An insight into limits: Understanding basic laws of Limits

Limits are used extensively in calculus and that’s why holds utmost importance in mathematics. A limit describes the action of a function near a threshold and operates the behavior of functions.

Most of the time, we plug in the value of limit in the function to know its behavior. Because of the complexities involved, sometimes, it becomes tricky to evaluate a function’s value by just applying the limit

Even though an online limit calculator could be very handy to deal with those complexities, we will explain basic limit rules and laws for a better understanding.

Limits – A formal definition

Let f(x) be defined for all x ≠ a over an open interval comprising a. Let L be a real number. Then,

$$\lim_{x \to a} f(x) = L$$

If, for every ε > 0, there exists a δ > 0, such that if \( 0 < |x−a| < δ, then |f(x) − L| < ε\).

Limits can be implemented to derivatives, integrals, sum, sequences, etc.

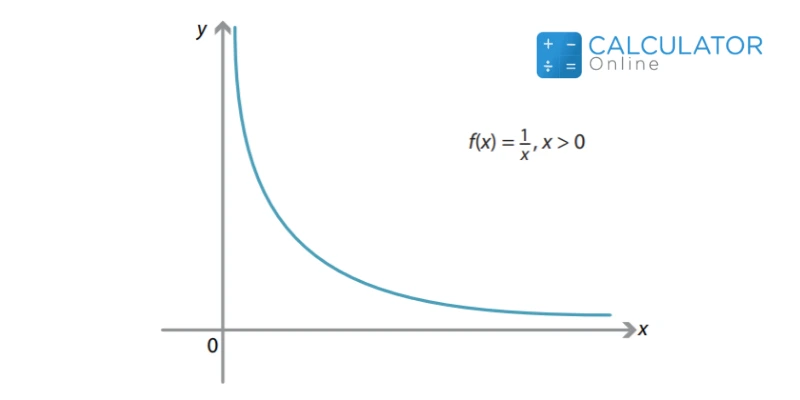
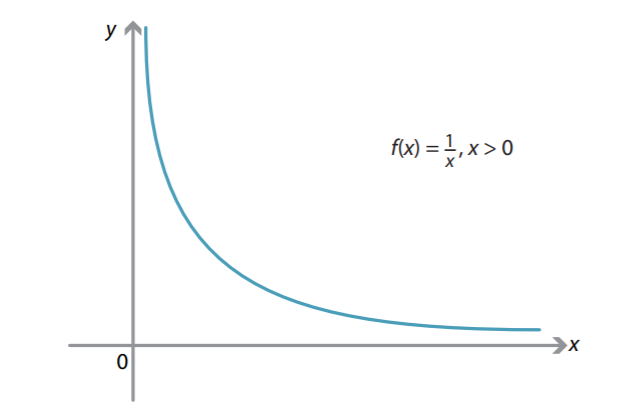
A graphical representation of limit for the function f (x) = 1/x for x > 0 would be like this.

Interpreting Limits Laws - Calculus

Rules of limits could be applied according to the algebraic operations such as sum, difference, root, etc.

To elaborate these laws, we will assume L, M, k, and c as real numbers while \(\lim_{x \to a} f(x) = L\) and \(\lim_{x \to a} g(x) = M\).

Moreover, for practical application, we will suppose that the function f(x) approaches a limit value of 5 and the function g(x) approaches a limit value of 8. So, L = 5 and M = 8.

1.Sum Rule

Sum rule of limits adds both functions and their limit values.

$$\lim_{x \to a} (f(x) + g(x)) = L + M$$

Let’s substitute limit values for both functions to see the effect of sum rule.

$$\lim_{x \to a} (f(x) + g(x)) = 5 + 8 = 13$$

2.Difference Rule

The difference rule should be applied when there is an expression containing a subtraction operation.

$$\lim_{x \to a} (f(x) - g(x)) = L - M$$

$$\lim_{x \to a} (f(x) - g(x)) = 5 - 8 = -3$$

3.Product Rule

For product, multiply the limit values to get the product of two functions approaching specifics limits.

$$\lim_{x \to a} (f(x) * g(x)) = L * M$$

$$\lim_{x \to a} (f(x) * g(x)) = 5 * 8 = 40$$

4.Constant Multiple Rule

If there is a constant multiplying with the function f(x), it will also be multiplied with the limit value.

$$\lim_{x \to a} (k * f(x)) = k * L$$

Suppose the constant in this case is 3.

$$\lim_{x \to a} (3 * f(x)) = 3 * 5 = 15$$

5.Power Rule

The power rule applies in the case of an exponential function.

$$\lim_{x \to a} (f(x))^n = L^n$$ 

n is a positive integer

Suppose n = 4.

$$\lim_{x \to a} (f(x))^n = 5^4 = 625$$ 

6.Root Rule

Limits can be applied on roots where n will be a positive number.

$$\lim_{x \to a} ^n\sqrt{f(x)} = ^n\sqrt{L} = L^{\frac{1}{n}}$$

n is a positive integer

Suppose n = 4.

 $$\lim_{x \to a} ^4\sqrt{f(x)} = ^4\sqrt{5} = 5^{\frac{1}{4}}$$

7.Quotient Rule

When dealing with quotients, we will divide the limits of both functions.

$$\lim_{x \to a}\frac{f(x)}{g(x)} = \frac{L}{M}$$

$$\lim_{x \to a}\frac{f(x)}{g(x)} = \frac{5}{8} = 0.625$$

Now that you know all of the above rules, let’s discuss L'Hopital's Rule which is significant considering the wide applications of limit calculator.

So, what did L'Hopital propose?

L'Hopital was a French mathematician who proposed that,

“When one function is divided by another function, the limit would be same if we take the derivative of each function.”

$$\lim_{x \to a} f(x) / g(x) = \lim_{x \to a} f'(x) / g'(x)$$

L'Hopital's Rule is a method to solve indeterminate or unspecified limits.

References

Michael Spivak, Calculus, 4th edition, Published, 2008.

Peter Brown, Limits and continuity, A guide for teachers.