How to write a number, equation, or polynomial in standard form

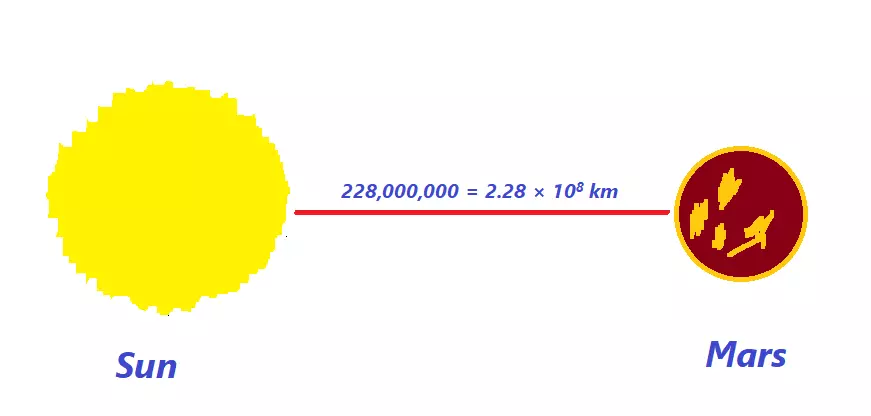
Standard form lets us easily read, write and understand a decimal number, an equation, or a polynomial. Imagine writing the distance of the sun from Mars. Would it be easy to read or write 228,000,000 km? Of course not.

What about 2.28 × 10⁸ km?

That’s where standard form comes in handy. The same goes for small numbers like the mass of an atom. Standard form or scientific notation (term used i the UK) is not only used for decimal numbers. We can also use it for

• Linear equations
• Quadratic equations
• Polynomials
• Decimal numbers

We can simply use a standard form calculator to convert a number into standard form.

However, if you find it difficult to do it by yourself, keep reading this post because we are going to explain how to convert a number, equation, or polynomial in standard form.

Standard Form of a Number:

We will go through an example to understand how to write numbers in standard form?

An atom is composed of three particles which are electron, proton, and neutron. A proton weighs 0.00000000000000000000000000167 Kg.

That’s a very small number which could be pretty daunting to read or write. Imagine a scientist working on atoms. It would be a waste of time if the scientist has to write that number a few times.

Let’s save the scientist from a lot of extra work by converting the mass of the proton into standard form.

1. Move the decimal after the first non-zero number and remove all of the leading zeroes. The number will become,  1.67.

2. Count the total number of digits you have shifted the point. In this case, we have moved the decimal to left for 27 places.
3. Place the multiplication sign and 10 with the number we got in 1^st step.

1.67 x 10

4. Raise -27 to the power of 10 to get the standard form.

1.67 x 10 ^-27

Now, we can effortlessly use this number regardless of it being a very small number.

Note: When raising a number as a power of 10, place a negative sign with power if you have moved the decimal from left to right. If you moved the decimal from right to left, the power (exponent) should be positive.

Standard Form of a Linear Equation:

Standard form of a linear equation is,

Ax + By = C

To make a standard linear equation, your equation should be in the above form. Here are the key points to consider linear equation and convert to standard form calculator.

• Both A and B could not be zero.
• A, B, and C should be integers.
• A cannot be negative.

Let’s apply these rules to a linear equation.

Example: 2y = 4x + 7

1. Take 4x to the left side of equation.

– 4x + 2y = 7

2. Multiply the whole equation with -1 to remove the negative sign with 4x.

 4x - 2y = -7

This equation is now in standard form. Where,

A = 4, B = -2, C = -7

Standard Form of a Quadratic Equation:

The standard form of a quadratic equation is,

Ax² + bx + c = 0

Let’s put a raw quadratic equation in standard form to understand the method.

Example: x(12 + x) = -5

1. Multiply x(12 + x).

12x + x² = -5

2. Move x² to the right side.

x² + 12x = -5

3. Move -5 to the left side of equation.

x² + 12x + 5 = 0

Where, a = 1, b = 12, c = 5

Standard Form of a Polynomial:

The concept behind the standard form of a polynomial is to write down the variable with the highest degree in the first place. By degree, we refer to the exponent of the variable.

Example: 5x² + 2x⁶ – 8 + 3x⁵ + 7x⁴

We will arrange the equation in descending order using the degree (exponent). In this case, 2x⁶ is the highest degree term.

2x⁶ + 3x⁵ + 7x⁴ + 5x² - 8

Final considerations:

The rules discussed above are different for each type of equation. You cannot apply the rules of a linear equation to make the standard form of a polynomial. You should be able to identify a polynomial, linear, or quadratic equation before converting to standard form.