Solving Antiderivatives by Using Integration Rules: Explained with Examples
In mathematics, antiderivatives are used to evaluate work, area, volume, or any other geometrical unit, or simply to calculate the area under the curve. It is a calculus topic used to calculate the indefinite integral as well as definite integral by using the fundamental theorem of calculus.
In this post, we will learn about the definition of antiderivative and how to solve antiderivative problems by using integration rules with a lot of examples.
What Is Antiderivative?
In calculus, antiderivative is the reverse process of the derivatives which means antiderivative reverses the results that a derivative does. That is why antiderivative is also known as inverse derivative or integral.
The antiderivative is mostly related to indefinite integral which is the type of the integral. Although antiderivative also relates with the definite integral which is another type of the integral through a theorem named as the fundamental theorem of calculus.
The opposite operation of differentiation is antidifferentiation which is the process of solving antiderivatives. Simply the process of calculating the antiderivatives of the functions is known as antidifferentiation or integration.
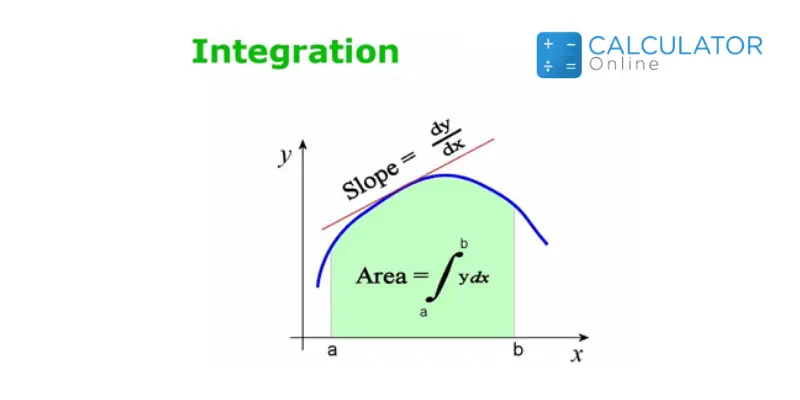
The notation for integral is a symbol “ʃ”. This notation is used for representing the integrals. If this symbol is present alone then we have to perform indefinite integral and if this symbol has upper and lower limits then we have to perform definite integral.

The antiderivative is not the same form of integral although it is a part of integral which is also said to be the indefinite integral. The antiderivative is also used in definite integral but it is applicable with the fundamental theorem of calculus.
Types of Antiderivatives:
The antiderivative is used to solve indefinite integral as well as a definite integral.
1.Indefinite Integral
The indefinite integral is used when the general antiderivative of a function has to be determined. Simply to determine the antiderivative of a function is called indefinite integral.
The reverse process of derivative is used to calculate the indefinite antiderivative of a function. Let there is antiderivative function F(x) of the given function f(x). Then,
ʃ f(x) dx = F(x) + C
Where C is the arbitrary constant known as the constant of integration or constant of antidifferentiation.
2.Definite Integral
The definite integral is used when the antiderivatives of a function have limits or have to determine among two endpoints. Simply to evaluate the antiderivative of a function among two endpoints is called a definite integral.
Let the function f(x) has to be evaluated among upper limit a and lower limit b then it is written with the help of the fundamental theorem of calculus as:
f(x) dx = (F(x))ba = F(b) – F(a)
Rules of Integration/Antiderivative:

|
Name of the Rule
|
Results of the Rules
|
|
(i) Power rule
|
ʃ xn dx= xn+1/n+1
|
|
(ii) Constant rule
|
ʃ A dx = Ax + C
|
|
(iii) Sum Rule
|
ʃ (f(x) + g(x)) dx= ʃ f(x)dx + ʃ g(x)dx
|
|
(iv) Difference Rule
|
ʃ (f(x) - g(x)) dx= ʃ f(x)dx + ʃ g(x)dx
|
|
(v) Product Rule
|
ʃ u.v dx = u ʃ v dx- ʃ u’(ʃ v dx)dx
|
How To Evaluate Antiderivative (Integral)?
For the calculation of antiderivatives problem, just keep the sound knowledge of its types and rules in your mind. However, to solve the antiderivative problems online, you can use an
antiderivative calculator which will provide you the correct result with steps.
In this section, we will go through a few examples to understand the process of integration or antiderivatives.
1.Indefinite Integral Example
2x5 - 4y2 + 7z
Solution:
Here, 4 rules will be used.
Power rule, Sum rule, Difference rule, and Constant rule.
Step 1: Write the given problem in integral notation.
ʃ (2x5 - 4y2 + 7z) dx
Step 2: Apply sum and difference rule.
ʃ (2x4 - 4y2 + 7z) dx = ʃ 2x5 dx - ʃ 3y2 dx + ʃ 7z dx
Step 3: Now apply constant rule.
ʃ (2x4 - 4y2 + 7z) dx = 2ʃ x5 dx - 3 y2 ʃ dx + 7z ʃ dx
Step 4: Apply power rule and solve the antiderivative.
ʃ (2x4 - 4y2 + 7z) dx = 2 (x5+1/5 + 1) - 3 y2 (x) + 7z (x)
ʃ (2x4 - 4y2 + 7z) dx = 2 (x6/6) – 3xy2 + 7xz
ʃ (2x4 - 4y2 + 7z) dx = x6/3 – 3xy2 + 7xz
2.Definite Integral Example
(6x4 + 3x) dx
Solution:
Step 1: Apply difference rule.
(6x4 + 3x) dx = 6x4 dx - 3x dx
Step 2: Take constant outside.
(6x4 + 3x) dx = 6 x4 dx - 3x dx
Step 3: Apply the power rule.
(6x4 + 3x) dx = 6(x4+1/4 + 1)61 – 3(x1+1/1 + 1)61
= 6 - 3
= 6/5 - 3/2
Step 4: Apply
limits using calculus theorem.
f(x) dx = (F(x))ba = F(b) – F(a)
(6x4 + 3x) dx = 6/5 (66 - 16) – 3/2 (62 – 12)
(6x4 + 3x) dx = 6/5 (46656 - 1) – 3/2 (36 – 1)
= 6/5 (46655) – 3/2 (35)
= 6(9331) – 3(17.5)
= 55986 – 52.5
= 55933.5
3.Double Integral Example
(x4 + 3x2 – 2y) dx dy
Solution:
Step 1: First solve the integral with respect to x and apply the difference rule.
(x4 + 3x2 – 2y) dx dy = (x4 dx + 3x2 dx - 2y dx) dy
Step 2: Take constant outside, from the integral.
(x4 + 3x2 – 2y) dx dy = x4 dx + 33x2 dx – 2y dx) dy
Step 3: Apply the power rule.
(x4 + 3x2 – 2y) dx dy = ((x4+1/4 + 1)32 + 3(x2+1/2 + 1)32 – 2y(x)32) dy
= ( - 3 – 2y(x)32) dy
= (1/5 - – 2y(x)32) dy
Step 4: Apply limits using calculus theorem.
f(x) dx = (F(x))ba = F(b) – F(a)
(x4 + 3x2 – 2y) dx dy = (1/5 (35 – 25) – (33 – 23) – 2y(3 – 2)) dy
(x4 + 3x2 – 2y) dx dy = (1/5 (243 - 32) – (27 – 8) – 2y(1)) dy
= (1/5 (211) – (19) – 2y) dy
= (211/5 – 19 – 2y) dy
= (42.2 – 19 – 2y) dy
= (23.2 – 2y) dy
Step 5: Now solve the integral with respect to y, steps will be similar as above.
(x4 + 3x2 – 2y) dx dy = (23.2) dy - (2y) dy
(x4 + 3x2 – 2y) dx dy = 23.2 dy – 2y dy
= 23.2 (y)31 – 2(y1+1/1+1)31
= 23.2 (y)31 – 2(y2/2)31
= 23.2 (y)31 – (y2)31
= 23.2 (3 – 1) – (32 – 12)
= 23.2 (2) – (9 – 1)
= 46.4 – 8
(x4 + 3x2 – 2y) dx dy = 38.4
Conclusion:
In calculus, the antiderivative is used to solve indefinite integral as well as a definite integral. You should be well versed with the types and rules of integration to solve the problems related to this topic. Once you grab the basic concepts of antiderivatives, you can easily solve any type of antiderivatives.