Polynomial Function
A polynomial function in general is the simplest form of a mathematical function, commonly most used in algebraic expressions with specific conditions. The highest power present in the polynomial function depends on the degree that it has in it. A polynomial function involves non-negative integer powers as well as positive integer exponents of a variable in an equation as the same quadratic equation, cubic equation, etc.
What is a polynomial function?
In mathematical form, the definition of polynomial functions can be defined as:
“A function that is expressed in the form of the algebraic polynomial equation”
The word polynomial is derived from two generic words poly and nomial. Since "Poly" means many, and "nomial" means the term, and when they are combined, we can say that the definition polynomial function includes "algebraic expressions with many terms."
Degree of polynomial functions
Generally, a polynomial number is represented as P(x). The highest power in the polynomial equation of the variable of P(x) is called its degree. A polynomial function’s degree is very important because it tells us about the behavior of the function P(x) when x becomes very large. The domain of a polynomial function is considered real numbers (R). Here, you can use our online
multiply polynomials calculator to find out algebraic expressions’ products with the blink of an eye.
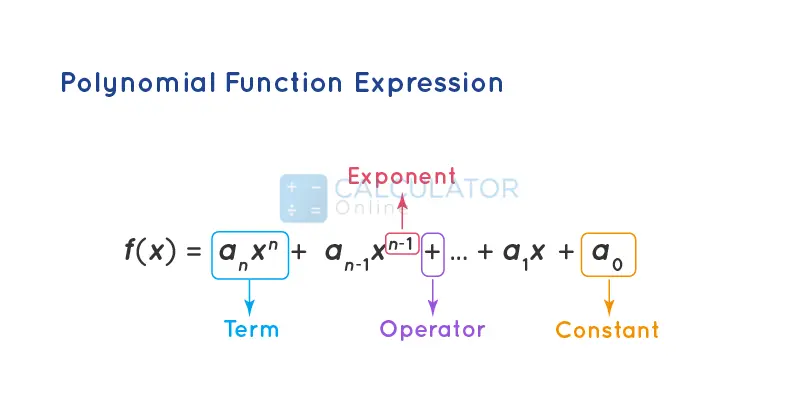
Polynomial function formula in standard form
Polynomial expression in standard form is given as:
$$ P\left(x\right) = a_{n}x^{n} + a_{n-1}x^{n-1} + … + a_{2}x^{2} + a_{1}x + a_{0} $$ then for x << 0, $$ P\left(x\right) ≈ a_{n}x^{n} $$
Thus, the polynomial algebraic expression contains variables of varying degrees, coefficients, positive exponents, and constants.
Polynomial Function Examples
Since a polynomial function contains positive integers as represented in the form of exponents. Here are some examples of polynomial functions that are related to arithmetic operations for such functions as addition, subtraction, multiplication, and division.
Types of Polynomial Functions
Let’s now discuss various types of polynomial equations that are based on the degree of the polynomial.
Constant Polynomial Function:
A constant Polynomial Function has no degree.
P(x) = a = ax^0
Zero Polynomial Function:
A function is expressed in the form f(x) = 0, is known as zero polynomial
Example:
P(x) = 0; where all as are zero, i = 0, 1, 2, 3, …, n.
Linear Polynomial Function:
A function that has the highest power is a 1 degree linear polynomial
Example:
P(x) = ax + b
Quadratic Polynomial Function:
A function that has the highest power is 2 degrees is called a quadratic polynomial
Example:
P(x) = ax^2+bx+c
Cubic Polynomial Function:
A function has the highest power is 3 degrees is called a cubic polynomial.
Example:
ax^3+bx^2+cx+d
Quartic Polynomial Function:
A function that has the highest power 4 degrees is called quartic polynomial
Example:
ax^4+bx^3+cx2+dx+e
Moreover, if you are trying to resolve problems regarding variables for the division of a polynomial by binomial, an online
polynomial long division calculator is the best choice to proceed with the calculations.
How to Determine a Polynomial Function?
Whether you desire how to determine if a function is a polynomial or not, the polynomial function equation is required to be checked against conditions for the exponents of the variables. These conditions are given bellowed:
-
The exponent of the variable in the function must be a non-negative whole number in every term. i.e., the exponent of the variable must not be a fraction or negative number in the function.
-
The variable of the function should not be under a radical form i.e, it should not contain any square roots, cube roots, etc.
-
The variable should not be in the form of a denominator.
The given table shows polynomial function equation examples and some non-examples of polynomial functions:
|
Functions
|
Variables
|
Exponents
|
Polynomial function or not?
|
|
f(b) = 4b2 – 6b + b3 – 15
|
b
|
2 in b2;
3 in b3
|
Yes
|
|
f(x) = x2/3+ 2x
|
x
|
2/3 in x2/3 ;
1 in 2x
|
No
|
|
f(y) = 1/y3
|
y
|
-3 in 1/y3
|
No
|
Graphing Polynomial Function:
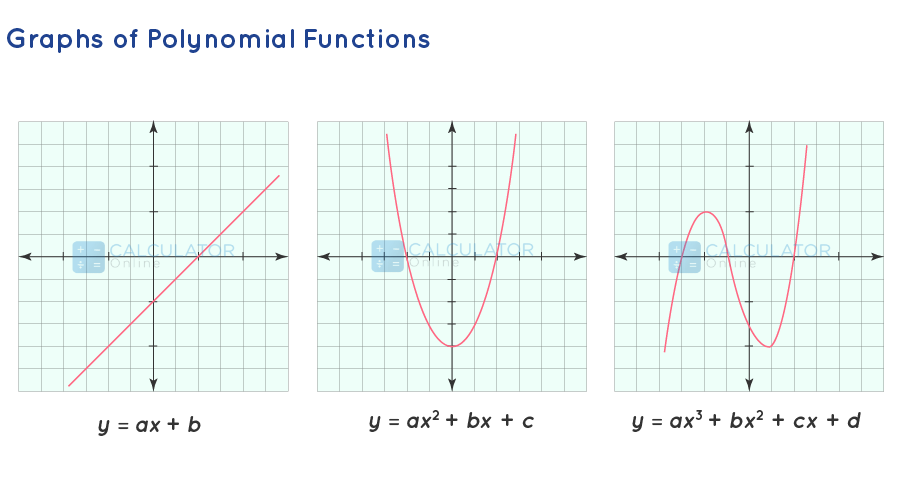
Now let us discuss all the polynomial functions in the form of a graph. As you know that the domain of any polynomial expression is the set of all real numbers. Bellow's given image represents the polynomial function graph and recognizes the relationship between equations and graphs.
-
In case a linear polynomial function is represented in the form y = ax + b then it shows a straight line.
-
In case a quadratic polynomial function is represented in the form y = ax^2 + bx + c then it shows a parabola.
-
A cubic polynomial function is represented in the form y = ax^3 + bx^2 + cx + d.then it shows a hyperbola.
Give a try to use this
slope Calculator to find the graph of a slope line and also shows step-by-step calculations.
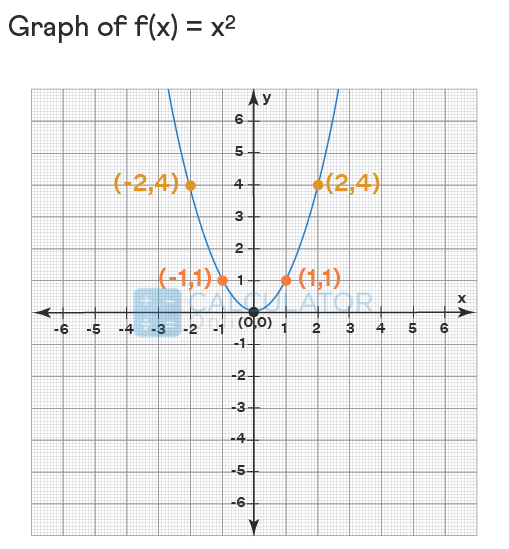
Example of the polynomial function graph
In a simple polynomial equation graph, we make a table that has some random values of x and the corresponding values of f(x). Here, we plot the points from the table and combine them with a curve line.
Let’s now draw the graph for the quadratic polynomial function f(x) = x^2.
|
x
|
-2
|
-1
|
0
|
1
|
2
|
|
f(x) = x2
|
4
|
1
|
0
|
1
|
4
|
Plot the points and then join them by a curve line by extending it on both sides to obtain the graph of the polynomial function.