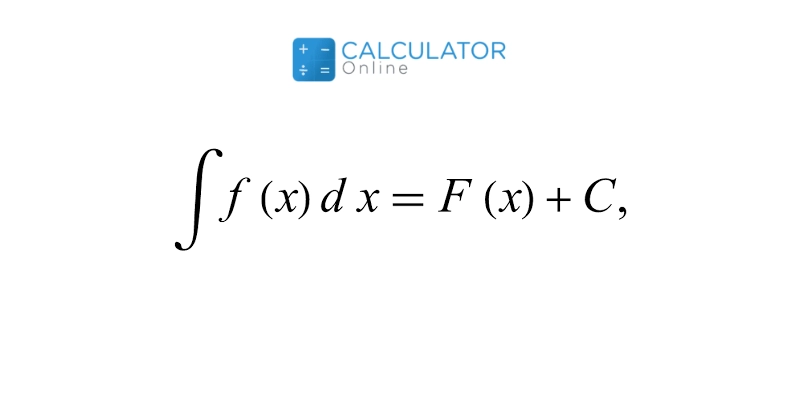Integration

Integration in math:

"The method to find a function g(x) of the derivative Dg(x) that is equal to the given function g(x) is termed as integration"

Representation:

This is denoted by the integral sign “∫,” as in ∫f(x) and usually considered the indefinite integral of the function. Users can use an online indefinite integral calculator regarding upper or lower limits to perform calculations swiftly and also get results in all integration formulas PDF form.

The symbol dx indicated a small displacement with respect to x; so ∫f(x)dx is the summation of the product of f(x) and dx. Also, you can perform calculations with respect to dx of f(x) with the assistance of an online derivative calculator.

The integration represents the summation of individual data. The integral formulas is usually calculated to find the functions of the area, displacement, and volume that occurs due to a collection of small data, which cannot be measured singularly.

Integration Formulas:

“The reverse process of differentiation and result becomes into inverse differentiation is considered a basic integration formula”

Basically, integration is a method of combining the part to find a whole. The integral formulas include:

Basic integration formulas for class 12
Class 12 integration formulas of trigonometric ratios
Inverse trigonometric functions
Product of functions
Advanced sets of all integration formulas

Formula of integration:

The general and simple integration formula is given as:

∫ f'(x).dx = f(x) + C

Basic Integration Formula list:

Using the fundamental theorems of special integrals formula, there are particularly integration basic formulas that are describes below as:

∫ xn.dx = x(n + 1)/(n + 1)+ C
∫ 1.dx = x + C
∫ ex.dx = ex + C
∫1/x.dx = log|x| + C
∫ ax.dx = ax /loga+ C
∫ ex[f(x) + f'(x)].dx = ex.f(x) + C

Standard integration formulas of Trigonometric functions:

When it comes to trigonometric functions, integration all formulas can be written simply in integrable form. Here is a special integration formula list of trigonometric and inverse trigonometric functions. These are:

∫ cosx.dx = sinx + C
∫ sinx.dx = -cosx + C
∫ sec2x.dx = tanx + C
∫ cosec2x.dx = -cotx + C
∫ secx.tanx.dx = secx + C
∫ cosecx.cotx.dx = -cosecx + C
∫ tanx.dx =log|secx| + C
∫ cotx.dx = log|sinx| + C
∫ secx.dx = log|secx + tanx| + C
∫ cosecx.dx = log|cosecx - cotx| + C

Integration Formulaes of Inverse Trigonometric Functions:

Let’s discuss the integral formulas of inverse trigonometric functions that are also related to the integration formula class 12. These are include:

∫1/√(1 - x2).dx = sin-1x + C
∫ /1(1 - x2).dx = -cos-1x + C
∫1/(1 + x2).dx = tan-1x + C
∫ 1/(1 +x2 ).dx = -cot-1x + C
∫ 1/x√(x2 - 1).dx = sec-1x + C
∫ 1/x√(x2 - 1).dx = -cosec-1 x + C

Advanced formulas of integration:

Here you will learn the all formulas of integration with respect to logarithm that are explained as under:

∫1/(x2 - a2).dx = 1/2a.log|(x - a)(x + a| + C
∫ 1/(a2 - x2).dx =1/2a.log|(a + x)(a - x)| + C
∫1/(x2 + a2).dx = 1/a.tan-1x/a + C
∫1/√(x2 - a2)dx = log|x +√(x2 - a2)| + C
∫ √(x2 - a2).dx =1/2.x.√(x2 - a2)-a2/2 log|x + √(x2 - a2)| + C
∫1/√(a2 - x2).dx = sin-1 x/a + C
∫√(a2 - x2).dx = 1/2.x.√(a2 - x2).dx + a2/2.sin-1 x/a + C
∫1/√(x2 + a2 ).dx = log|x + √(x2 + a2)| + C
∫ √(x2 + a2 ).dx =1/2.x.√(x2 + a2 )+ a2/2 . log|x + √(x2 + a2 )| + C

Different maths Integration Formulas:

There are generally 3 types of integration methods and each method has its own unique technique to find the integrals. These are include:

Integration by parts formula:

“Whether the product of two functions give, you can apply the integration by parts formula or partial integration to calculate the value of integral”.

Formula:

The integration formulas for class 12 while using partial integration is given as:

∫ f(x).g(x) = f(x).∫g(x).dx -∫(∫g(x).dx.f'(x)).dx + c

Example: ∫ xex dx is written in the form ∫ f(x).g(x).

Now apply the appropriate integration formula and calculate the integral value.

f(x) = x and g(x) = ex

Thus ∫ xex dx = x∫ex .dx - ∫( ∫ex .dx. x). dx+ c

= xex - ex + c

However, use an online double integral calculator that gives the resultant values for both definite and indefinite double integrals regarding the algebra system.

Integration by substitution formula:

“When a function becomes a function of an another, then you can apply the integration formula for substitution”

Formula:

If I = ∫ f(x) dx, where x = g(t) so that dx/dt = g'(t), then can write as dx = g'(t)

This can be written I = ∫ f(x) dx = ∫ f(g(t)) g'(t) dt

Example: Consider ∫ (3x +2)4 dx

You can use the integration formula of substitution to calculate the value.

Let u = (3x+2). ⇒ du = 3. dx

Thus ∫ (3x +2)4 dx =1/3. ∫(u)4. du

= 1/3. u5 /5 = u5 /15

= (3x+2)5 /15

To calculate the triple integral values of a given function, an online triple integral calculator is also available for you to perform calculations instantly.

Integration by partial fractions formula:

If you need to find the integral of P(x)/Q(x) which is an improper fraction and the degree of P(x) < that of Q(x), then you can use integration by partial fractions. Here the partial fraction decomposition as P(x)/Q(x) = T(x) + P1 (x)/ Q(x), where T(x) is a polynomial in x and P1 (x)/ Q(x) is a proper rational function.

Besides, an online improper integral calculator will help you to measure the integral with defined limits and you can aslo get integration formulas PDF form.