Rational Numbers

What Is a Rational Number In Math?

In mathematics form, a rational number can be defined as:

“A number that is written in the form of p/q, where p and q are integers, and q is not equal to zero”

In other words, we can say that rational numbers can be expressed as a fraction where the denominator and numerator are integers and the denominator is not equal to zero. If you endeavour to resolve problems regarding rational numbers, you can make use of the free rational or irrational calculator for instant and detailed computations.

Example:

Rational numbers examples are as follows:

p	q	p/q	Rational
1	3	1/3	0.3333
4	5	4/5	0.8
2	4	2/4	0.5

Keep scrolling down and learn more information about what's a rational number.

Brief Explanation:

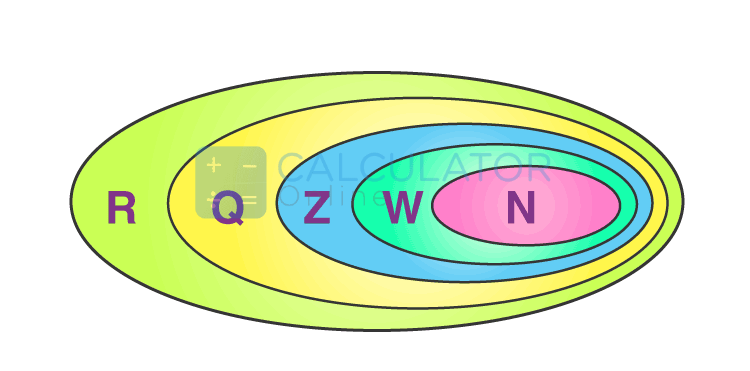
In arithmetic form, a rational number can be denoted as the form of quotient p/q of two integers and q ≠ 0. All the integers are included in the set of rational numbers and each of which can be expressed as a quotient with the integer in the form of the numerator and 1 as the denominator. When a rational number is divided, the given result will become in the decimal form either terminating or repeating decimals.

Look at the above figure. What do you see? Do not panic if you do not get an idea about it as we will explain it. In the figure:

R represents the “Real number” that includes rational numbers, integers, whole numbers, and natural numbers.
Q represents “Rational number” that includes integer, whole number, and natural number but may or may not include a real number.
Z represents “integers” that includes whole numbers and natural numbers but may or may not include real numbers and rational numbers.
W represents “Whole numbers” that include natural numbers but may or may not include real numbers and integers
N represents “Natural numbers” that may or may not include natural numbers, real numbers, and integers.

Types of rational numbers

Now, we discuss four types to solve all rational numbers:

Integers:

“An integer can be changed into a fraction which is a rational number”.

If you trying to resolve problems with integer values, you can make to use the free integer calculator quickly.

Example:

4 can be written as 4/1. Since both the numerator (4), as well as the denominator (1), are integers and the denominator is not equal to 0. Hence, 4 is a rational number.

Fractions Made up of Integers:

“Any fraction that is made of integers is considered a rational number, and the denominator is not equal to 0”

Example:

1/4, -5/2, and 27/-465, shows that all rational numbers are integers.

Terminating Decimal Numbers:

“A decimal number that terminates or ends at some point is also a rational number”.

Example:

Take the decimal number 0.5 which is converted to 2/4, which is a rational number.

Non-terminating Decimal Numbers With Infinitely Repeating Patterns:

“Decimal numbers that give repeating values infinitely are rational numbers”

Example:

Take the fraction value 1/6, its result will come to 0.16666, the pattern of 6’s after the decimal point repeats infinitely that is why it considered a rational number.

What Does Rational Mean In Standard Form?

Standard Form of Rational Numbers can be defined as:

“The numerator and the denominator have no common factors other than 1 and its denominator is always a positive integer”.

Example:

Consider 15/45 which is a rational number and it can be simplified by division into 1/3, which means that common factors between the numerator and the denominator have only one. Hence, 1/3 is a rational number in the standard form.

Positive and Negative Rational Numbers:

The rational number can be described as either positive or negative. The rational number will be positive when both p and q are positive integers. While if the rational number takes in the form of -(p/q), then p or q is a negative integer. It means that

-(p/q) = (-p)/q = p/(-q)

Now, let's discuss the common difference between positive and negative rational numbers.

Positive Rational Numbers	Negative Rational Numbers
Both the numerator and denominator are the same sign	Numerator and denominator are of opposite signs
All are greater than 0	All are less than 0
Examples: 13/15, 8/10, and 4/5	Examples: -3/19, 9/-13, and -1/5.

Arithmetic operations on Rational numbers

In mathematics, basic arithmetic operations are performed by rational numbers on integers.

To solve the arithmetic operations. Let us suppose p/q and a/s

Addition:

“When we add p/q and a/s, it is necessary to make the denominator the same”

p/q + a/s = (p+a)/qs

Example:

1/4 + 3/8 =(2+3)/8 = 5/8

Subtraction:

“Similarly, if you subtract p/q and a/s, you need to make the denominator same, first, and then do the subtraction”

p/q - a/s = (p - a)/qs

Example:

3/4 - 2/8 = (6-2)/8 = 4/8 = 1/2

Multiplication:

While multiplying two rational numbers, both the numerator and denominator of the rational numbers are multiplied respectively.

p/q * a/s = pa/qs

Example:

1/4 × 5/4 = (1×5)/(4×4) = 5/16

Division:

If p/q is divided by a/s, then it is represented as

(p/q)÷(a/s) = ps/qa

Example:

1/4 ÷ 3/8 = (1×8)/(4×3) = 8/12 = 2/3

Multiplicative Inverse:

“The reciprocal of the given fraction is the multiplicative inverse of the rational number”

Example:

6/7 is a rational number, then its multiplicative inverse is 7/6, therefore (6/7)x(7/6)=1

Rational Numbers Properties:

A rational number is a subset of the all real number since the rational number will follow all the properties of the real number system. Following are some important properties of rational numbers:

If we multiply, add, or subtract any two rational numbers, then the result will become a rational number.
In case we divide or multiply both the numerator and denominator with the same factor, the result will remain the same.
When we add zero to a rational number, then we will get the same number itself.
Generally, rational numbers are closed under addition, subtraction, and multiplication form.

How to find a rational number between two rational numbers?

No doubt, there are infinite numbers of rational numbers between any two rational numbers. By using two different methods, you could easily find rational numbers between two rational numbers. Right now, let us have a look at the two different methods.

Method 1:

In the 1st method, we find out the identical fraction for the given rational numbers and then find out the rational numbers in between them. The required numbers should be rational numbers.

Method 2:

In the 2nd method, we find out the mean value for the two given rational numbers. The mean value should be required for a rational number. If you want to find more rational numbers, then repeat the same process with the old and newly obtained rational numbers.

Besides that, you can also find rational expression forms with the assistance of a rational expression calculator instantly.

Solved Examples:

Example 1:

Identify each of the following as what are rational numbers or irrational: 2/5, 80/13008, 15, and √7.

Solution:

For 2/5

2/5 is a rational number as it can be expressed in the form of a fraction. 2/5 = 0.4

For 80/13008

Fraction 80/13008 is rational.

For 15

15, also be written as 15/1. Again a rational number.

For √7

Value of √7 = 2.64575….. It is a non-terminating value and hence cannot be written as a fraction form. Therefore it is an irrational number.

Example 2:

Identify whether a mixed fraction, 1 ¾ is a rational number.

Solution:

The Simplest form of 1 ¾ is 7/4

Numerator = 7, which is an integer

Denominator = 4, is an integer and not equal to zero.

So, 7/4 is a rational number.

Are negative numbers rational?

Yes, negative numbers are rational numbers as they include all integers both positive as well as negative integers.

What is the difference between rational and irrational numbers?

A rational number is expressed as the ratio of two integers, and the denominator is not equal to zero. On the other hand, irrational numbers are represented in the form of fractions.

Is 0 a rational number?

Yes, 0 is a rational number as it is an integer, written in any form like 0/1, 0/3, where q is a non-zero integer. It can be expressed in the form of p/q= 0/1.

Is 3.14 a rational number?

Yes, 3.14 is a rational number because it has a terminating value. But is not a rational number because the exact value is 3.14159265358979323 which is non-terminating and non-recurring.