Permutation and Combination

Permutation vs Combination

In mathematical form, permutations and combinations can be defined as:

Permutation:

“The arrangement of several objects in a specific order taken in which tiny detail does matter at a specific time”

There are two types of math permutations and are given as:

Repetition is Allowed:

Example: Number lock such as, it could be “2-2-2”.

No Repetition Allowed:

Example: The first four people in a race. You can’t be first, second, and third at the same time.

Combination:

"A way of selecting the objects from a set or collection in which the order of selection doesn’t matter is termed a math combination".

It allows only choosing elements that matter. It means the order in which elements are chosen is not essential.

There are two types of math combinations and are given as:

Repetition is Allowed:

Example: coins in your pocket (2, 6, 6, 10, 10)

No Repetition Allowed:

Example, lottery numbers (2, 14, 16, 28, 35, 48)

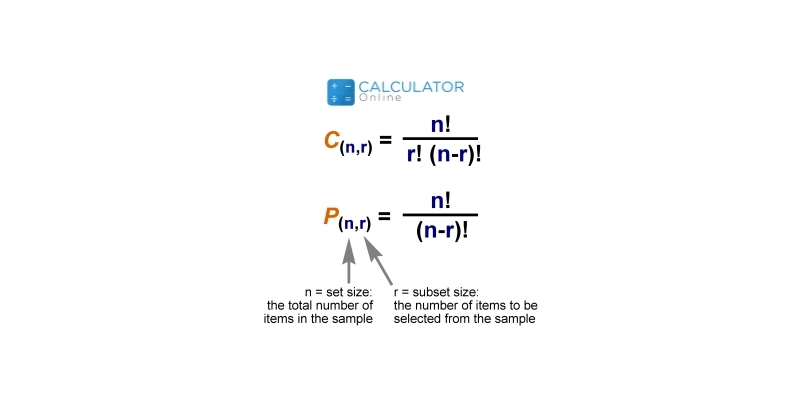
Permutation and combination formula:

Permutation formula:

The representation of K in the formula contains objects that taken from a set of n things with no replacement and the order of tiny detail does matter.

nPk = n!/(n − k)!

Combination Formula:

While in a combination, the option of k items from a set of n objects taken without replacement and order of set does not matter. Sometimes the terms k-selection or k-combination with repetition are often used.

nck = n!/k!(n − k)!

Permutation & Combination: Derivation

Let’s assume the derivation of combination and permutation formula with the help of an example and is described under as:

Derivation of Permutation Formula:

Consider that there are r boxes, and each of them can hold one item. There will be many permutations that are described by the no. of ways to fill in r vacant boxes by n items.

No. of ways will be filled to the first box: n
Similarly, no. of ways in the second box can be filled: (n – 1)
Same as, no. of ways be filled to the third box: (n – 2)
Likewise, no. of ways can be filled the fourth box as: (n – 3)
No. of ways for rth box can be filled: [n – (r – 1)]

Hence, the number of permutations of n objects are taken r at a specific time, where 0 < r ≤ n and the objects do not repeat again i.e., n(n – 1)(n – 2)(n – 3) . . . (n – r + 1)

⇒ nPr = n(n – 1)(n – 2)(n – 3). . .(n – r + 1)

The above equation then multiply and divide by (n – r) (n – r – 1) . . . 3 × 2 × 1 to get results

Derivation of Combination Formula:

Let us suppose that there are r boxes, and each of them can hold one thing.

No. of ways to select the first object from n distinct objects is given: n
Likewise, no. of ways that the second object selected from (n-1) distinct objects: (n-1)
Similarly, no. of ways to choose the third object from (n-2) distinct objects: (n-2)
As given above, no. of ways to select rth object from [n-(r-1)] distinct objects: [n-(r-1)]

Completing the selection of r objects from the original set of n things makes an ordered subset of r elements. The number of ways to make a selection of r elements of the original set of n elements is given as:

n (n – 1) (n – (n-3) . . . (n – (r – 1)) or n (n – 1) (n – 2) … (n – r + 1).

Besides, you can calculate the factorial (n!) of a given n positive number by using an online factorial calculator.

Difference between permutation and combination:

Let’s read the given below table to understand the difference between combinations and permutations. These are:

Combinations	Permutations
Combinations are commonly used to observe the number of possible groups which can be formed.	Permutations are used when order/sequence is needed to arrange.
They have similar kinds of items.	They contain typically different kinds of objects.
Generally, two things from the given things taken such as a, b, c are ab, bc, ca	Two things from three given things like a, b, c is ab, ba, bc, cb, ac, ca
Different possible selections of 'r' things are taken from 'n' things.	In permutations, different possible arrangements containing 'r' objects are taken from 'n' things.

Difference between Permutations and Combinations Examples:

If you want to know the difference between permutations vs combinations to clarify your concept related to math combinations permutations. Look at the examples of permutation vs combination and they are given as:

Permutations:

Arrangement of people, numbers, digits, alphabets, letters, words, and colours etc.
Selecting a team lead captain or keeper and a particular one from a group.
Choose two favourite colours, in order, from a colour book.
Picking first, second and third prize winners in the race.

Combinations:

Select the menu, food, clothes, subjects, team etc.
Choose the three team members from a group.
Select two colours from a colour book.
Picking three prize winners only.