Types of Polygons

What is a polygon?

In geometric form, shapes that are polygons can be defined as:

“Two-dimensional closed shape bounded by line segments (straight line) and does not has curved sides is termed a polygon”

Polygon is a mixture of two words, poly means “many” and gon means “sides”.

Since each side of a polygon is its edge point and generally, it does not have a curved side. The points or corners where two sides meet each other are the vertices of a polygon.

Polygon shape sides:

Generally, polygons are edged by a distinct number of line segments. let’s have a look at the shapes of different polygons given as under:

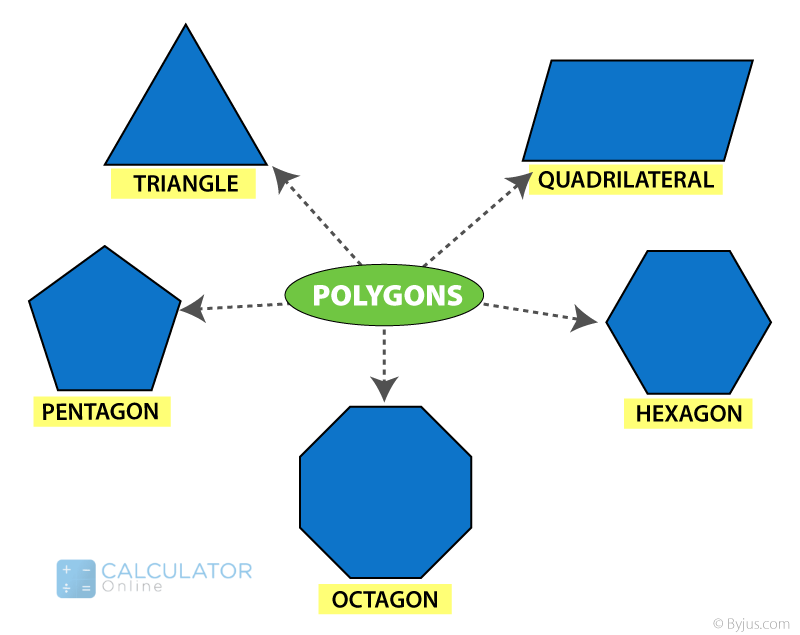
Different types of polygons:

The polygon shape sides are classified into different types which depend on the sides and angles. These include:

Regular Polygon:

A specific type of polygon in which all the sides and interior angles are measured equal to each other is known as a regular polygon

Examples:

A square
An equilateral triangle
A rhombus

Irregular polygon:

A type of polygon in which all of its sides, as well as the interior angles, have different measurements is known as irregular polygon

Examples:

A scalene triangle
A rectangle
A kite

Convex Polygon:

A particular type of polygon in which the measure of all its interior angles results in a resultant angle less than 180 degrees is termed convex polygon.

Examples:

A signboard
A football
A circular plate

Concave Polygon:

A polygon that has one or more interior angles that measure more than 180 degrees in resultant angle is called a concave polygon.

Examples:

A star
A spoon

However, you can find out all the sides as well as all interior angles of any polygon kind with the help of an online polygon calculator instantly.

Angle of Polygons:

As we know, different polygons have multiple vertices and sides. Since each corner of the vertex in a polygon shape names has a specific measurement of angles. Therefore, these angles are classified into two types.

Interior Angle:

The sum of all the interior angles of a polygon with ‘n’ number of sides is given as:

Sum = (n − 2)π radians

Exterior Angle:

The sum of the exterior angles of a polygon becomes equal to 360°

Formula:

Interior angle + Exterior angle = 180 degrees
Exterior angle = 180 degrees – Interior angle

Note: If the polygon is regular or irregular, the vertex of a different polygons is the sum of an interior angle and exterior angle which is equal to 180°

Moreover, you can also calculate the interior and exterior angle of a polygon by using a double angle calculator to perform calculations swiftly.

Properties

Let’s now discuss the properties of the shapes that are polygons depends on the sides and angles. These includes:

The sum of all the interior angles of a polygon that is n-sided can be measured by the formula as (n – 2) × 180°.
The number of diagonals in a polygon shape with n sides is given by the formula as n(n – 3)/2
The number of triangles assembled by joining the diagonals from one point of the vertex can be measured by the given formula as n – 2
Each interior angle of an n-sided regular polygon can be measured by the formula as [(n – 2) × 180°]/n
Each exterior angle of an n-sided regular polygon can be measured by the formula as 360°/n

Shapes that are polygons:

Let’s discuss the polygon shape names that are given below:

Triangles

Now you must be thinking about is a triangle a polygon. Yes, it is! Let us explain how!

Triangle is one of the types of polygons and can be defined as:

“In the simplest form, the polygon with 3 sides and 3 vertices has termed a triangle”

However, based on the sides and angles, triangles are categorized into different types of polygons:

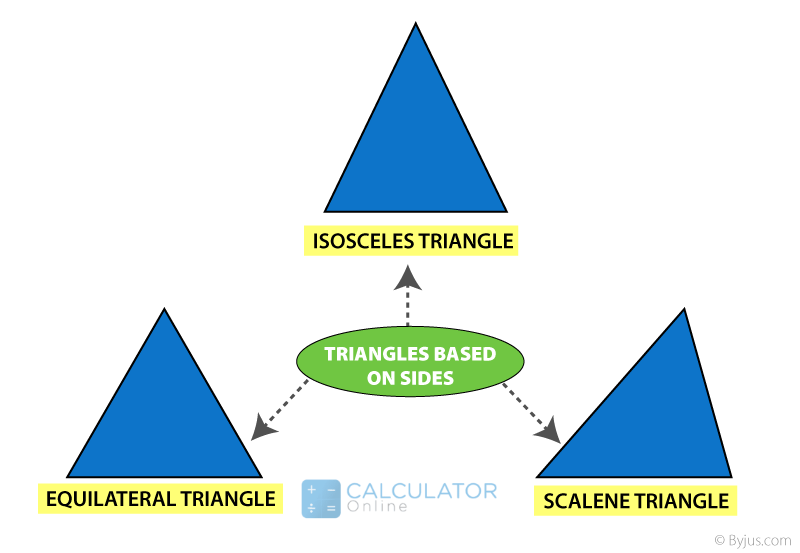
Triangles (polygon with 3 sides) – Based on Sides:

Equilateral triangle:

“A triangle that has all sides and angles are equal in measurements is an equilateral triangle”

Isosceles triangle:

“A triangle in which two sides are equal but the angles are opposite to each other is an isosceles triangle”

Scalene triangle:

“A triangle in which all the 3 sides of a triangle are unequal is a scalene triangle”

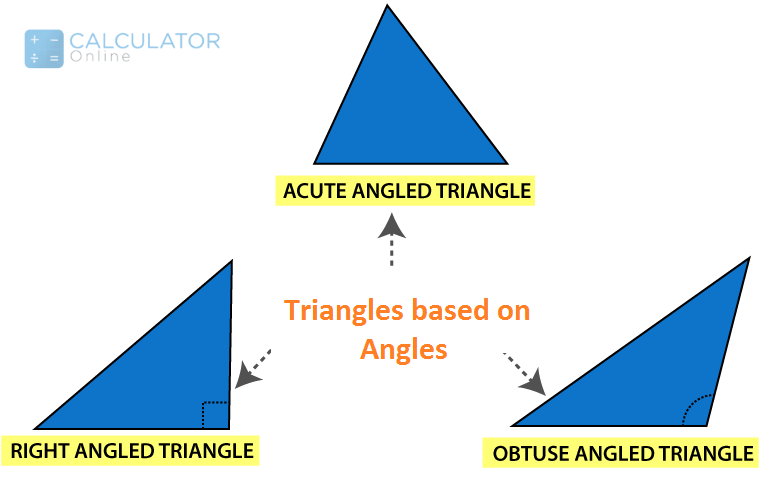
Triangles (polygon with 3 sides) - Based on Angles:

Acute angled Triangle:

Each angle in the triangle is less than 90° degree

Right Angled Triangle:

One of the three angles in the triangle is equal to 90° degree

Obtuse Angled Triangle:

One angle in the triangle is greater than 90° degree

A free online triangle calculator assists you to calculate all the angles and sides for any given triangles.

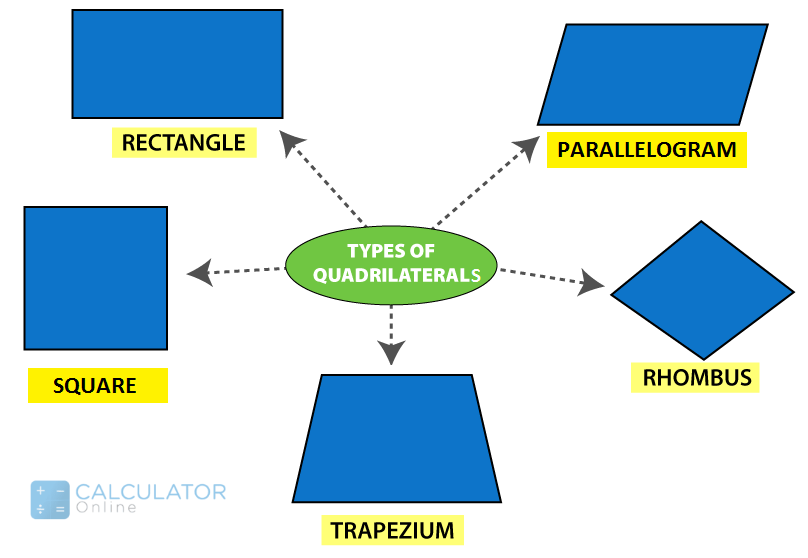
Quadrilaterals:

“A polygon having four equal sides is termed a quadrilateral”

Generally, a polygon is formed by bounded four-line segments such that they meet each other to make 4 angles.

A quadrilateral polygon names are classified into the following:

Square
Rectangle
Parallelogram
Rhombus
Trapezium

Image of Quadrilaterals

Here you can determine the sides and angles with accurate results by using an online parallelogram calculator within no minutes.

Names of polygons

Let’s discuss a list of polygons that clarify your concept about the shapes that are polygons

Polygon names	No. of Sides	No. of Diagonal	No. of vertices	Interior Angle
Triangle	3	0	3	60
Quadrilateral	4	2	4	90
Pentagon	5	5	5	108
Hexagon	6	9	6	120
Heptagon	7	14	7	128.571
Octagon	8	20	8	135
Nonagon	9	27	9	140
Decagon	10	35	10	144
Hendecagon	11	44	11	147.273
Dodecagon	12	54	12	150
Triskaidecagon	13	65	13	158.308
Tetrakaidecagon	14	77	14	154.286
Pentadecagon	15	90	15	156

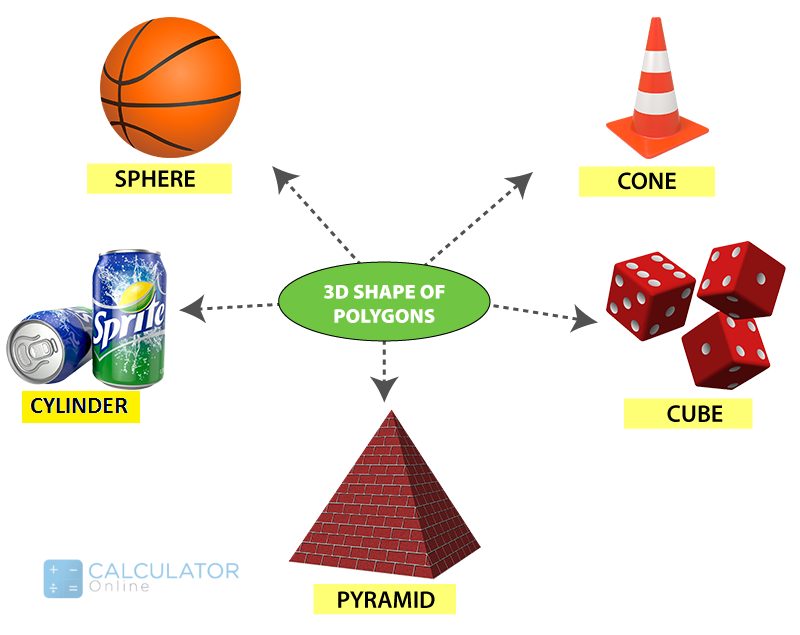
Three Dimensional Shapes that are polygons (3-D shape)

"A solid object that is made by the combination of two or more polygons and 2d shapes is known as three-dimensional shape"

Look at the picture of the names of polygons and observe 3d shapes in real-life examples:

What shape has 6 sides and 6 vertices?

In geometry, a hexagon is one of the different polygons that has closed two-dimensional plane with 6 sides and 6 angles. Hexa means six and gonia means angles

Generally, polygons to be studied in the first few years at school level as a basic introduction of geometry and mathematics. Students find it easy to understand different types of polygons and and can enjoy to learn the shapes that are polygons and name of polygons.