Triangle Calculator

The triangle calculator helps to determine the unknown angles, side lengths, median, and much more with ease making trigonometry problem-solving a seamless experience.

Triangle Facts:

• A triangle can not have more than one vertex (a point at which two or more line segments or edges or curves met) with an internal angle greater than 90 degrees
• The sum of the interior angles is always equal to 180 degrees
• The sum of the two interior triangles is equal to the exterior angles of the triangle
• Depending on the interior angles and length of sides, we have six types of triangles as right Angle Triangle, the Acute Angle Triangle, the Obtuse Angle Triangle, the Isosceles Triangle, the Scalene Triangle, the equilateral triangle, etc.

How To Calculate The Height And Area of A Triangle?

Height of the Triangle:

The equation that is used to find the height of the triangle is as follows:

\(\ h=\ 2(\dfrac{A}{b})\)

Where

• A represents the area
• b is the length of the base

Area of Triangle:

Calculate the area of a triangle by using the following formula:

\(\ Area =\dfrac{1}{2}bh\) 

Where

• b is the base 
• h is the height of the triangle

There is another way to calculate the area of triangle and it is known as Heron’s formula. It uses the sides of the triangle to find the area. Let’s take a look!

\(\ s=\dfrac{a+b+c}{2}\)

\(\ Heron’s\ Formula=\ area=\sqrt{s(s-a)(s-b)(s-c)}\)

How Do You Find The Sides And Angles of A Triangle?

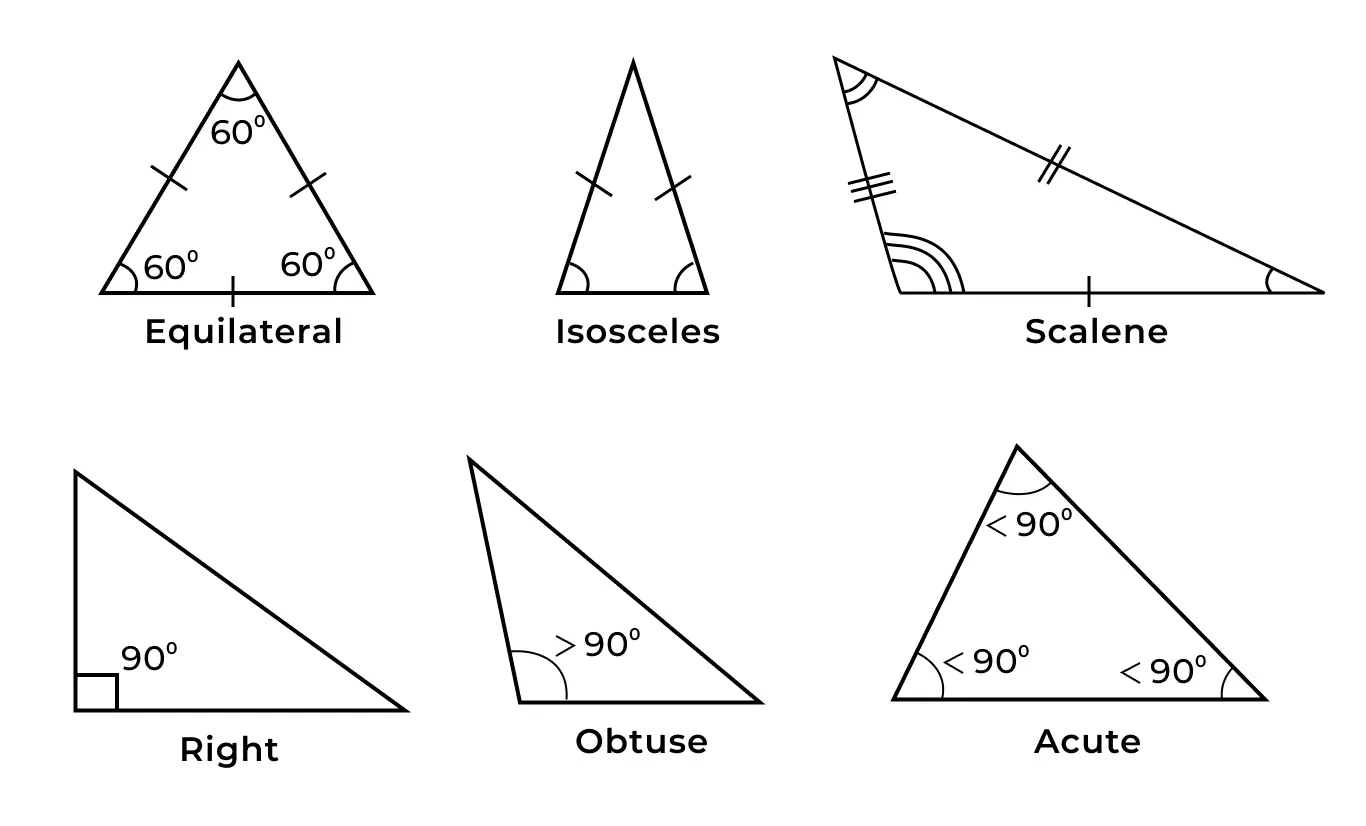
Triangles are polygons having three vertices.

Using the Pythagorean theorem, the Law of Sines, and the Law of Cosines, you can find the sides and angles of the triangles.

The Law Of Sine:

By using the law of sine, you can easily find any side of a triangle or the missing angle of a triangle without any hurdle.

\(\frac{a}{sin\left(A\right)} = \frac{b}{sin\left(B\right)} = \frac{c}{sin\left(C\right)}\)

If the triangle angles and the hypotenuse are given, then use the law of sines to get the side lengths of the right triangle as follows:

a = c × sin(α) or a = c × cos(β)

b = c × sin(β) or b = c × cos(α)

Pythagorean Theorem:

If any two sides of a right triangle are known you can easily find the third side with the help of this theorem which states:

\(\ a^{2}+b^{2} =\ c^{2}\)

If you know any of the two sides of the right triangle, simply use the Pythagorean theorem.

When side a is missing, transform the equation as:

\(\ a =\sqrt{\ c^{2}-b^{2}}\)

To find For hypotenuse c:

\(\ c =\sqrt{\ a^{2}+b^{2}}\)

Law of Cosines:

The law of cosines states:

\(\ a^{2} =\ c^{2} + \ b^{2} -\ 2bc\ cos A\), solving for cos A,  \(\cos A =\dfrac{\ b^{2}+c^{2} – a^{2}}{2bc}\)

\(\ b^{2} =\ a^{2} + \ c^{2} -\ 2ca\ cos B\), solving for cos B,  \(\cos B =\dfrac{c^{2}+\ a^{2}-b^{2}}{2ca}\)

\(\ c^{2} =\ b^{2} + \ a^{2} -\ 2ab\ cos C\),   solving for cos C, \(\cos C =\dfrac{a^{2}+\ b^{2}-c^{2}}{2ab}\)

Find The Missing Sides of A Triangle Using Trigonometric Functions:

If one triangle angle and one side are given:

a = b × tan(α)

b = a × tan(β)

If the triangle area and one side of the triangle are given:

\(\ area =\dfrac{a\times\ b}{2}\)

When the area of the right triangle and the length of side a are given then the equation will be as follows:

\(\ b =\dfrac{2\ \times\ area}{a}\)

\(\ c =\sqrt{a^{2}+(\dfrac{2\times\ area}{a})^{2} }\)

How To Calculate The Inradius And Circumradius?

Inradius:

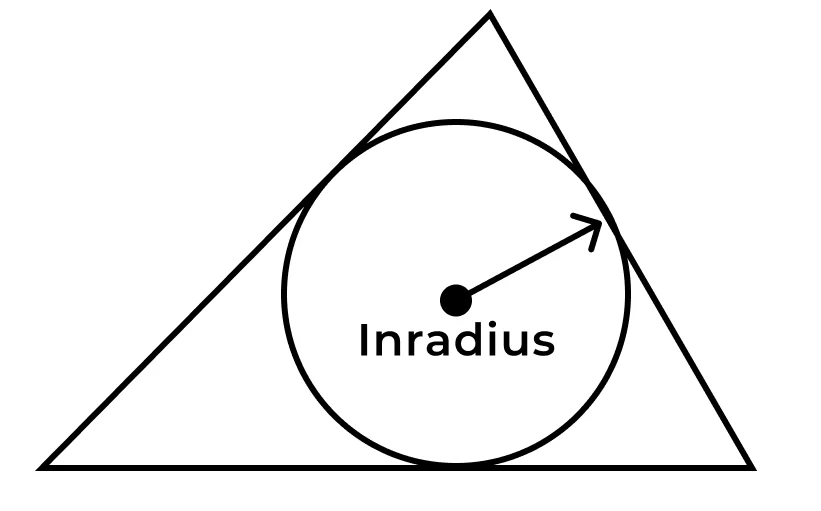
It is the radius of the inscribed circle. In general, it’s the circle that can fit inside the triangle and it is perpendicular to each side of the polygon. 

Use the below-mentioned formula to calculate the inradius of a triangle:

\(\ r=\dfrac{Area}{semiperimeter}\)

Circumradius:

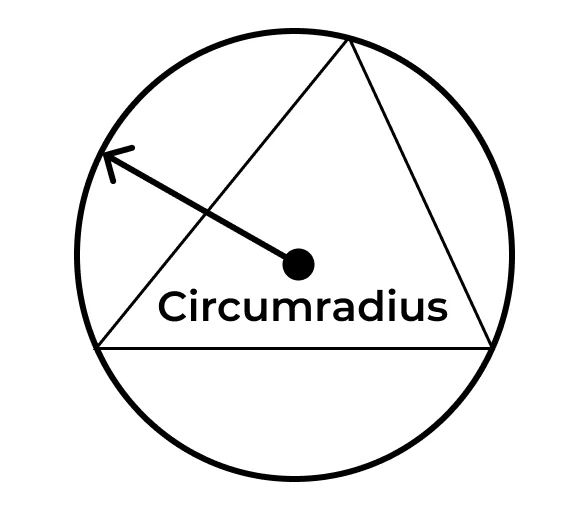
As the name shows it is the radius of the circumscribed circle. It is the minimum size of the circle that can fit inside the triangle.

Let’s see the following formula that is used to calculate the circumradius of the triangle:

\(\ R=\dfrac{a}{2sin(a)}\)

Example:

Predict a triangle along with its terms with the following given information:

• \(\ a = 2\)
• \(\ m∠A = 60^{o}\)
• \(\ m∠B = 20^{o}\)

Solution:

As we are given two angles and one side, let us start!

Step # 01 (Find Angle of Triangle):

\(\ m∠C = 180° – A – B\)

\(\ m∠C = 180^{o} – 60^{o} – 20^{o}\)

\(\ m∠C = 100^{o}\)

Now converting all angles into radians as follows:

\(\ m∠A = 60^{o}\times \frac{π}{180}\)

\(\ m∠A = 60^{o}\times \frac{3.14}{180}\)

\(\ m∠A = \frac{188.4}{180}\)

\(\ m∠A = 1.0472\ rad\)

Similarly:

\(\ m∠B = 20^{o}\times \frac{π}{180}\)

\(\ m∠B = 20^{o}\times \frac{3.14}{180}\)

\(\ m∠B = \frac{62.8}{180}\)

\(\ m∠B = 0.34907 rad\)

Likewise:

\(\ m∠C = 100^{o}\times \frac{π}{180}\)

\(\ m∠C = 100^{o}\times \frac{3.14}{180}\)

\(\ m∠C = \frac{314}{180}\)

\(\ m∠C = 1.74533\ rad\)

Step # 02 (How To Find The Side of A Triangle?):

As we are given only one side, we need to find the length of the triangle sides. Calculate triangle sides as follows:

\(\ b = \frac{a\times sin(B)}{sin(A)}\)

\(\ b = \frac{2 \times sin(0.34907)}{sin(1.0472)}\)

\(\ b = 0.78986\)

Similarly, we have:

\(\ c = \frac{a\times sin(C)}{sin(A)}\)

\(\ c = \frac{2 \times sin(1.74533)}{sin(1.0472)}\)

\(\ c = 2.27432\)

That’s how you can find the missing side of a triangle but you can easily depict the unknown sides of the triangle with the help of the calculator.

Step # 03 ( Calculating The Triangle Area):

\(\ A = \frac{ab.sin(C)}{2}\)

\(\ A = \frac{2\times0.78986.sin(1.74533)}{2}\)

\(\ A = 0.77786\)

Step # 04 (Calculating Perimeter And Semiperimeter):

\(\ Perimeter=\ p = a + b + c\)

\(\ Perimeter=\ p = 2 + 0.78986 + 2.27432\)

\(\ Perimeter=\ p = 5.06418\)

Similarly:

\(\ Semiperimeter=\ s = \frac{a + b + c}{2}\)

\(\ Semiperimeter=\ s = \frac{2 + 0.78986 + 2.27432}{2}\)

\(\ Semiperimeter=\ s = 2.53209\)

Step # 05 (Calculation of Heights of Triangle Sides):

We can determine the height of each side as given below:

\(\ Height=\ h_{a}=\frac{2 \times { Area}}{a}\)

\(\ Height=\ h_{a}=\frac{2 \times 0.77786}{2}\)

\(\ Height=\ h_{a} = 0.77786\)

Now we have:

\(\ Height=\ h_{b}=\frac{2 \times { Area}}{b}\)

\(\ Height=\ h_{b}=\frac{2 \times 0.77786}{0.78986} = 1.96961\)

\(\ Height=\ h_{b} = 1.96961\)

Similarly:

\(\ Height=\ h_{c}=\frac{2 \times { Area}}{c}\)

\(\ Height=\ h_{c}=\frac{2 \times 0.77786}{2.27432} =\)

\(\ Height=\ h_{c} = 0.68404\)

Step # 06 (Determining Medians Of Each Side):

\(\ Median=\ m_{a}=\sqrt{(\frac{a}{2})^2 + c^2 – ac.cos(B)}\)

\(\ Median=\ m_{a}=\sqrt{(\frac{2}{2})^2 + 2.27432^2 – 2\times2.27432.cos(0.34907)} = 1.37775\)

Similarly:

\(\ Median=\ m_{b}=\sqrt{(\frac{b}{2})^2 + a^2 – ab.cos(C)}\)

\(\ Median=\ m_{b}=\sqrt{(\frac{0.78986}{2})^2 + 2^2 – 2\times0.78986.cos(1.74533)}\)

\(\ Median=\ m_{b} = 2.10482\)

Now we have:

\(\ Median=\ m_{c}=\sqrt{(\frac{c}{2})^2 + b^2 – bc.cos(A)}\)

\(\ Median=\ m_{c}=\sqrt{(\frac{2.27432}{2})^2 + 0.78986^2 – 0.78986\times2.27432.cos(1.0472)}\)

\(\ Median=\ m_{c} = 1.00936\)

Step # 07 (Finding Inradius):

\(\ Inradius=\ r=\frac{area}{s}\)

\(\ Inradius=\ r=\frac{0.77786}{2.53209}\)

\(\ Inradius\ r=0.3072\)

Step # 08 (Finding Circumradius):

\(\ Circumradius\ R=\frac{a}{2.sin(A)}\)

\(\ Circumradius\ R=\frac{2}{2 \times sin(1.0472)}\)

\(\ Circumradius\ is\ 1.1547\)

Other Languages:  Výpočet Trojúhelníku, Calculer Triangle, Dreieck Rechner, Kalkulator Segitiga, Kalkulator Trójkata, Калькулятор Треугольника, Calcular Triangulo, Üçgen Hesaplama, Calculadora De Triangulos