Math Calculators ▶ Pythagorean Theorem Calculator
Adblocker Detected
We always struggled to serve you with the best online calculations, thus, there's a humble request to either disable the AD blocker or go with premium plans to use the AD-Free version for calculators.
Disable your Adblocker and refresh your web page 😊
The online Pythagorean Theorem calculator helps to calculate the length of any missing sides (a, b, or c) of a right triangle. Also, you can be able to find the area of a right triangle by using this free online calculator. The Pythagorean Theorem solver will solve the Pythagoras equation and provides you a step-by-step solution.
Get ready to understand how to do Pythagorean theorem calculations and the basics of the Pythagorean theory.
In mathematics, the Pythagorean theorem belongs to Euclidean geometry. It represents the relationship between three sides of a right triangle. It states that the square of the hypotenuse (c) is equivalent to the sum of the squares of the other two lengths of sides (a and b) of a triangle.
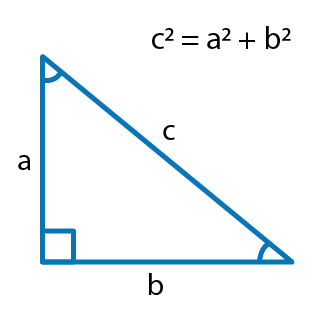
According to the definition, the Pythagorean Formula is:
\[c^2= a^2 + b^2\]
In this Pythagorean Theorem equation:
To find the unknown value of any side, another form of the same formula can also be applied. Algorithms of Pythagorean Theorem calculator usually apply the following arrangement of formula whenever you need to calculate the missing side of the right-angled triangle.
However, Use an online Law of Cosines Calculator that helps to find unknown length of sides or angles of a triangle.
We can understand the use of the Pythagorean theorem to calculate the missing side of the right triangle as follows:
Example:
In any right-angled triangle if a is equal to 4 and b is equal to 8, what will be the value of c?
Solution:
In manual calculations, We can use the Pythagorean formula to calculate the missing side of the right triangle.
We have:
Put the values and proceed the step by step solution as follows:
However, if you are using a Pythagorean calculator, then you don’t have to remember the formula as it will deliver you a step-by-step solution and gives you the output in some standard units along with the values of other dynamics of right angle and the area of a triangle.
A Pythagorean Theorem formula can be modified in three possible forms to calculate three different sides of the triangle.
To find the length of hypotenuse “c” we will apply:
\[c = \sqrt{a^2 + b^2}\]
So if a = 2 and b = 2 we can have the following step by step solution to figure out the missing value.
$$c = \sqrt{a2 + b2 }$$
$$c = \sqrt{a^2+ b^2}$$
$$c = \sqrt{4 + 4} = \sqrt{8}$$
$$c = 2$$
To find the length of side b:
\[ b = √c2 – a2\]
So if \(c =4\) and \(a = 2\) then:
To find the length of side a:
\[a = \sqrt{c^2 – b^2}\]
If we have \(c = 6 \)and\( b = 2\) then:
\[a = \sqrt{6^2 – 2^2}\]
\[a = \sqrt{36 – 4} = \sqrt{32}\]
\[a = 5.65\]
To find the area of a right triangle we have to multiply the side “a” and “b” and then divide the answer by 2.
If the side a = 4 and side be = 4 we can calculate the area of a right triangle as follow:
$$A = 4 x 4 / 2$$
$$A = 16 / 2$$
$$A = 8$$
Other than the manual calculation you can use a Pythagorean Theorem calculator to find out the area of a right triangle by entering the lengths of the side “a” and “b” of a triangle.
Furthermore, An online Law of Sines Calculator allows you to find the remaining angles and lengths of sides of a triangle.
A Pythagorean triple represents a set of three positive integers. These integers are represented by a, b, and c. Pythagorean triple follows Pythagoras theorem formula:
The simplest set of integers is 3, 4, and 5. However, we have some other possible sets as well.
Example:
$$7^2+ 24^2= 25^2$$
$$49 + 576 = 625$$
$$625 = 625$$
Hence it proves that 7, 24, and 25 are the Pythagorean triples according to the rule.
With This Pythagorean calculator you can figure out the sides “a”, “b” hypotenuse c, and area A by entering any two known values to find the third value in a simple way as follows:
Input
Output:
The Pythagorean Theorem Calculator displays the following results against the given values
There are many situations in real life where you can apply the Pythagorean theory. For example, to find the required length of a ladder to reach the top of the building from the point where you are standing apply the Pythagorean theorem formula. As in this situation, the length of the building and your distance from the building are known values.
The Pythagorean Theorem equation is known as the crown jewel of mathematics. We cannot say that this theorem is 100% true or false. its validity and reliability always depend on the given conditions.
No; such lengths cannot create a triangle. As a matter of fact, to create a triangle the sum of the two sides must be larger than the length of the third side. However, if the length of any two sides is known then the third one can be calculated via the Pythagoras theorem calculator.
For the past 2500 years, it is the most well-known theorem around the globe. It helped human beings to evolve as its application is everywhere, whether it is a construction, a bench, a graph with axes, or the even atomic structure of any crystal. A Pythagorean theorem solver helps in all these aspects to calculate the unknown third dimension.
Hence, with this Pythagorean Theorem calculator, we learned about the unknown lengths of sides and the area of a right-angled triangle. The pythagorean formula plays a significant role in various areas of real life. After understanding the concept of Pythagorean theory you can use this Pythagorean theorem solver to skip hectic calculations. it provides its support for learning as well as educational purpose anywhere and anytime without any cost.
From the source of Wikipedia: Forms of the theorem, Euclid’s proof, Dissection and Rearrangement.
From the source of Math Planet: The Pythagorean Theorem, Dissection without Rearrangement, Consequences and uses of the theorem.
From the source of Cut the Knot: Pythagorean Theorem, Pythagorean proposition, Dissection using inscribed circle.
Everybody needs a calculator at some point, get the ease of calculating anything from the source of calculator-online.net. Feel free to contact us at your convenience!
