Area of A Sector Calculator

An online area of a sector calculator is specifically programmed to find the area of the sector, the arc length, and chord length of a circle sector. This free calculator generates accurate outputs so you may not feel any difficulty during your calculations. But before we move further, let us make sure that you need to memorize some crucial terms which are as follows.

Stay Focused!

What Is A Sector Of The Circle?

In the context of geometry:

“A specific figure that is bounded by an arc connecting with one end of two radii separately is called sector of a circle”

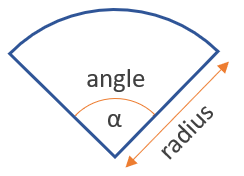
In the following figure:

• The curved line represents the arc of the sector
• The two straight lines connected at right angle(\(\alpha\))to each other are called radii.
• If we convert the arc into the straight line, we will be getting a chord of the circle.

The area of sector calculator finds all of the above mentioned values in a span of time to save your precious time.

Important Formulas:

Here we will be discussing some formulas that are used to find these geometrical terms. These include:

Area Of Sector Formula:

You can easily determine the area of a sector of a circle with the help of sector area formula given below:

$$ \text{Area Of Sector} = \frac{\alpha * r^{2}}{2} $$

Where:

\(\alpha\) = angle of a sector
r = radius of the sector

Arc Length Formula:

You can use the following formula to determine the length of any arc of the sector:

$$ \text{Arc Length} = \theta * r $$

Chord Length Formula:

Below is the most optimized formula to determine the chord length of the sector of a circle.

$$ \text{Chord Length} = 2*r*sin\frac{\theta}{2} $$

Here if you ever get stuck during calculations of these quantities, try using the free online area of a sector calculator. You will always get accurate answers regarding each term that you wish to find.

How To Find The Area Of A Sector Of A Circle?

Let us solve a couple of examples to help you in better understanding of the concept.

Example # 01:

The radius of a circle sector is 3cm. The internal radii angle is \(45\text^{o}\). How to find area of a sector?

Solution:

First we need to convert angle given in degrees to radians:

$$ \theta_{rad} = \frac{\text{Angle In Degrees} * π}{180} $$

$$ \theta_{rad} = \frac{45\text^{o} * 3.14}{180} $$

$$ \theta_{rad} = \frac{141.3}{180} $$

$$ \theta_{rad} = 0.785rad $$

Now using the area of a sector of a circle formula:

$$ \text{Area Of Sector} = \frac{\alpha * r^{2}}{2} $$

Putting the value given in the statement:

$$ \text{Area Of Sector} = \frac{0.785 * \left(3\right)^{2}}{2} $$

$$ \text{Area Of Sector} = \frac{0.785 * 9}{2} $$

$$ \text{Area Of Sector} = \frac{7.065}{2} $$

$$ \text{Area Of Sector} = 3.53 cm^{2} $$

You can also get the same results with a free area of sector calculator in a glimpse of an eye to make your calculations more easy.

Example # 02:

What is the arc length of a circle constructed by radius of 4cm and angle of \(90^\text{o}\)?

Solution:

We know that:

$$ \theta_{rad} = \frac{\text{Angle In Degrees} * π}{180} $$

$$ \theta_{rad} = \frac{\(90^\text{o}\) * 3.14}{180} $$

$$ \theta_{rad} = \frac{3.14}{2} $$

$$ \theta_{rad} = 1.57rad $$

$$ \text{Arc Length} = 1.57rad * 4cm $$

$$ \text{Arc Length} = 6.28cm $$

Here the free sector area calculator automatically determines the same value even if you go for calculating the area of a sector of a circle.

How Area Of A Sector Calculator Works?

This free area of sector calculator is considered the most optimized way of determining the authentic results corresponding to sector area. Let us guide you how to use it properly:

Input:

In the input section, we have the following values available:

• Central angle
• Radius
• Diameter
• Sector area
• Arc length
• Chord length

What you need to do is that:

• Enter any two values from all above mentioned
• Hit the calculate button

Output:

The free area of a sector of a circle calculator calculates:

• Sector area
• Arc length
• Chord length

FAQ’s:

Can area of sector formula be used to find area of quadrant?

No, you can not solve for quadrant areas by using arc area formula. To solve this term, subject to the formula below:

$$ \text{Area Of Quadrant} = \frac{π*r^{2}}{4} $$

Is the sector angle same for every sector?

Not at all! The sector angle varies with the area of the sector that could be measured with the help of area of a sector formula..

For example:

Quadrants have a sector angle of \(90^\text{o}\).
Sextants have a sector angle that measures to be \(60^\text{o}\)
In case we are dealing with octants, the angle is \(45^\text{o}\)

In case of any difficulty, you can use sector area calculator for instant and precise outcomes.

What is the formula of the perimeter of the circle sector?

The addition of the arc lengths and those of both radii is called sector perimeter.

$$ \text{Perimeter Of The Sector} = 2 * R + [\frac{\theta}{360^\text{o}} * 2 * π * r] $$

What do you mean by the term Pi(π)?

It is basically the ratio of the circle’s circumference to its diameter

$$ π = \frac{\text{Circumference Of The Circle}}{Diameter} $$

Conclusion:

Geometrical analysis requires a very deep focus while carrying it out. Professionals, engineers, scholars, and architects always work to maintain accuracy in their results so as to avoid any difficult situation. That is why they make a vast use of the free online area of a sector calculator for finer outputs.

References:

From the source of Wikipedia:  Circumference, Circle, Ellipse

From the source of khan academy: Quadrants on the coordinate plane, Plotting a point

From the source of lumen learning: Angles, Converting Between Degrees and Radians, Finding Coterminal Angles