Hypotenuse of a Triangle Calculator

Use this online hypotenuse calculator that will help you to find the length of the hypotenuse of a right triangle in a fraction of a second. The hypotenuse of a triangle calculator can be determined hypotenuse by using either two sides, one angle, and side, or area and one side of a right-angled triangle. Let’s start to understand how to find hypotenuse and the length of the longest side of a right-angled triangle with the help of the hypotenuse formula.

What is a Hypotenuse of a Triangle?

In geometry, a hypotenuse is the longest side of the right-angled triangle, which is opposite to the 90-degree right angle.

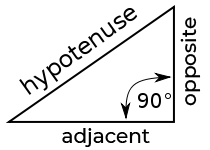
However, an Online Unit Circle Calculator helps you to find the sine, cosine, and tangent value for the angle that helps to figure out the coordinates on the unit circle.

Hypotenuse Formula:

The hypotenuse calculator uses different formulas according to known values to determine the longest side (c) of a triangle.

Solve the Hypotenuse with Two Sides:

Generally, the Pythagorean Theorem is used to calculate the hypotenuse from two different sides of the right-angled triangle.

If you know two sides then take a square root of the sum of squares:

Hypotenuse \((c) = \sqrt{ (a^2 + b^2)}\)

However, an online Pythagorean Theorem Calculator allows you to calculate the length of any missing sides of a right triangle.

Solve the Hypotenuse with One Side and the Adjacent Angle:

If you know one side and the adjacent angle, then the hypotenuse calculator uses the following formula:

Hypotenuse (C) = a / cos (β)

Where hypotenuse is equal to the side (a) divided by the cos of the adjacent angle β.

Solve the Hypotenuse using One Side and the Opposite Angle:

If you already know one side and the opposite angle of a right triangle, then an online calculator uses the following formula to solve the hypotenuse of right triangle:

Hypotenuse (c) = a / sin (a)

Where hypotenuse is equal to the side “a” divided by the sin of the opposite angle α.

How Hypotenuse Calculator Works?

An online hypotenuse of a triangle calculator 100% free and helps you to find the length of different sides of a triangle quickly. You just stick to these steps to get the precise measurements related to the length and angles of the right-angled triangle.

Input:

• First, select an option from a drop-down menu to calculate from two known values.
• Then, substitute the values in the relevant fields with units.
• Click the calculate button.

Output:

• The calculator provides the answer with a particular formula.
• The calculator displays your input and step-by-step calculations.

FAQ:

Is the hypotenuse (c) always the longest side of a right-angled triangle?

Yes, the hypotenuse (c) is the longest side of a right-angled triangle all the time. For isosceles triangles, two equal sides are called legs, while in the case of equilateral triangles all sides are known just as sides.

What should you need to do when hypotenuse is the opposite?

If the hypotenuse (C) is the opposite, then you are considering the wrong angle of the triangle. Consider one of the other angles (α or β) and the opposite side that does not form that particular angle.

How I can find the hypotenuse of isosceles triangles? 

Firstly, find the length of one of any non-hypotenuse sides and take a square.

Then, double the results and take the square root of these values. Thus, the answer is the length of the hypotenuse.

How we can solve a triangle with only the hypotenuse?

Well, we cannot answer a right-angled triangle with only the hypotenuse (C). The reason is the other two angles and sides are still unknown. Therefore the right triangle still has many forms.

Conclusion:

This online hypotenuse calculator is functioned to determine the length of any side of a right-angled triangle. It assists you when you desire to find any side or area of a triangle. This calculator is equally helpful both for students and teachers.

Reference:

From the source of Wikipedia: Etymology, Calculating the hypotenuse, Trigonometric ratios.

From the source of Story of Mathematics: Hypotenuse Leg Theorem, Proof of Hypotenuse Leg Theorem, right triangles.

From the source of Lumen: Trigonometry and Right Triangles, Right Triangles and the Pythagorean Theorem Finding a Missing Side Length, Trigonometric Functions, Sine, Cosine, and Tangent.

Other Languages: Hipotenüs Hesaplama.