Equation of a Circle Calculator

Find the equation of a circle against a certain input by using this free equation of a circle calculator. With that, obtain all related parameters that help in defining various properties of a circle by using this center and radius calculator.

What about going deeper in the concept to know more?

Give a read!

What Is A Circle?

In the context of geometry:

“A specific round figure with no edges is known as the circle”

Equation of A Circle:

The generic circle equation is a geometrical expression that is used to find each and every point lying on a circle. It is given as follows:

$$ \left(x-h\right)^{2} + \left(y-k\right)^{2} = r^{2} $$

Where:

\(\left(h, k\right)\) = coordinates of the center

\(r\) = radius of the circle

Standard Form:

Now if the centre coordinates of a circle equation are kept zero, then we get the standard form that is given as below:

Putting h = 0, k = 0;

$$ \left(x-0\right)^{2} + \left(y-0\right)^{2} = r^{2} $$

$$ \left(x\right)^{2} + \left(y\right)^{2} = r^{2} $$

You can also get an equation in its standard form by subjecting to our best circle equation calculator.

Parametric Form of The Circle Equation:

Just like various techniques involved in simplification of any problem, an equation of the circle also has various forms. Among these forms, parametric is the most important and is given as follows:

x = r * cos(α)

y = r * sin(α)

Where:

• x and y are the coordinates belonging to any point on the circle
• α is the angle that is made by the point with the center of the circle
• r is the radius by default

Now if you are willing to determine the parametric circle equation, then you need to replace the center of it by \(\left(h, k\right)\) and add to x and y, respectively:

x = h + r * cos(α)

y = k + r * sin(α)

Conversion Among Parametric and Standard Form of Equation:

Well, this section will highlight the relationship between both of the circle equation’s forms. The interesting fact here is that our free online equation of a circle calculator also aids in determining the related form of generic equation for a circle in moments. Let’s get ahead to perform a conversion:

Suppose you have the parametric form of the equation:

x = r * cos(α)

y = r * sin(α)

Or

cos(α) = x/r

sin(α) = y/r

Now if you recall first identity of trigonometry:

sin²(α) + cos²(α) = 1

Putting values of cos(α) and sin(α):

$$ sin^{2}\left(α\right) + cos^{2}\left(α\right) = 1 $$

$$ \left(\frac{y}{r}\right)^{2} + \left(\frac{x}{r}\right)^{2} = 1 $$

$$ \frac{y^{2}}{r^{2}} + \frac{x^{2}}{r^{2}} = 1 $$

Now multiplying the whole expression by r^{2}

$$ \frac{y^{2}}{r^{2}} * r^{2} + \frac{x^{2}}{r^{2}} * r^{2} = 1 * r^{2} $$

$$ y^{2} + x^{2} = r^{2} $$

Which is the standard form of the circle’s equation that could also be verified by using the standard equation of a circle calculator in the blink of an eye.

Alternative Form:

Here we have another generic form of the circle equation that is written below:

$$ x^{2} + y^{2} + Dx + Ey + F = 0 $$

It is actually the expanded form of the standard form and you can also get your answer in this form by the use of the equation of circle calculator.

Circumference:

Circumference is the length of the outer boundary of the circle. You can determine this parameter by using our another best circumference calculator. But manually, you can find this element by the following formula:

$$ C = 2*\pi*r $$

Area:

The area of a circle can be found by the following expression:

$$ Area = \pi*r^{2} $$

Here except the whole circle, you can determine the area of any particular sector by subjecting to our best area of a sector calculator.

Eccentricity and Local Eccentricity:

You must keep in mind that eccentricity and local eccentricity of a circle are always zero. This is because the circle is the ellipse in which we have two foci that coincide with its center. Moreover the distance of the foci from the center is always zero.

Domain:

The domain of any circle can be calculated by the following formula:

$$ Domain = [h-r, h+r] $$

Range:

Get going by determining the range of any equation with this expression:

$$ Range = [k-r, k+r] $$

In case you find these calculations lengthy enough, let our best equation of a circle calculator do these calculations for you in moments.

How To Find The Equation of A Circle?

What about resolving a couple of examples to know how to write the circle equation properly? Let’s move ahead!

Example # 01:

How to find equation of a circle with the center and radius given below:

$$ Center = \left(3, 7\right) $$

$$ Radius = 3 $$

Solution:

As we know that:

$$ \left(x-h\right)^{2} + \left(y-k\right)^{2} = r^{2} $$

Here h = 3, k = 7, radius = 3

Putting the values in the above equation:

$$ \left(x-h\right)^{2} + \left(y-k\right)^{2} = r^{2} $$

$$ \left(x-3\right)^{2} + \left(y-7\right)^{2} = 3^{2} $$

$$ \left(x-3\right)^{2} + \left(y-7\right)^{2} = 9 $$

Which is the required equation.

Example # 02:

What would be the center of the expanded form of the circle equation given

$$ \left(x-4\right)^{2} + \left(y-2\right)^{2} = 5^{2} $$

Solution:

As the given equation is:

$$ \left(x-4\right)^{2} + \left(y-2\right)^{2} = 5^{2} $$

Comparing it with the general equation:

$$ \left(x-h\right)^{2} + \left(y-k\right)^{2} = 5^{2} $$

We get:

$$ center = \left(h, k\right) $$

$$ center = \left(4, 2\right) $$

The best center of a circle calculator also calculates the center in a fragment of seconds.

Now moving ahead to expand the given equation:

$$ \left(x-4\right)^{2} + \left(y-2\right)^{2} = 5^{2} $$

$$ \left(x^{2} + 16 – 8x\right) + \left(y^{2} + 4 – 4y\right) = 25 $$

$$ x^{2} + 16 – 8x + y^{2} + 4 – 4y -25 = 0 $$

$$ x^{2} + y^{2} -8x -4y -5 = 0 $$

The free equation of a circle calculator also goes for determining the same results but saving you a lot of time. Now what do you think?

How Equation of A Circle Calculator Works?

This center radius form calculator takes a couple of seconds to determine a circle equation along with various parameters associated. Let’s find how!

Input:

• From the first drop down list, go for selecting the parameters with which you want to perform calculations
• After you make the selection, enter all the required elements in their designated fields
• Tap the calculate button

Output:

The free equation of the circle calculator calculates:

• Standard form of the circle equation
• General form of the circle equation radius of the circle
• Diameter of the circelke
• Area of the circle
• Circumference of the circle
• Domain and range of the circle
• Eccentricity and local eccentricity of the circle
• Center coordinates for the circle
• Parametric form of the circle equation
• Graph of the equation given

FAQ’s:

What is circle theorem?

This theorem states that:

“If we are having three points on the circle’s circumference just say A, B, and C and AC is the diameter of the circle, then the triangle made by joining all the three points would be the right angled”

What is the secant of the circle?

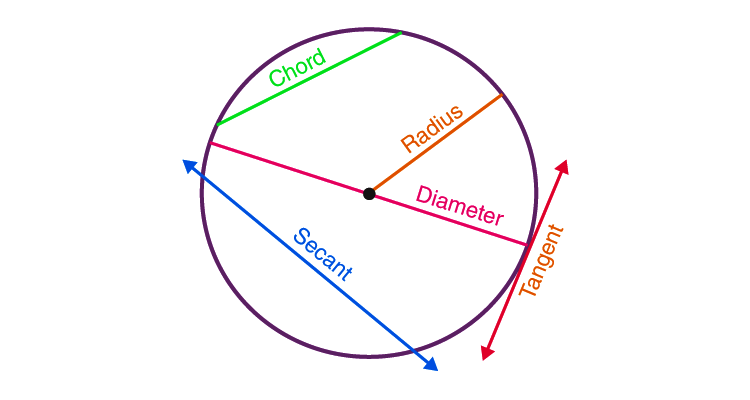
A particular line intersecting the circle at two different points is called a secant line.

Are all radii of a circle equal?

Yes, of course they are!. As the center of the circle is equidistant from all the points on the circumference, this means all the radii are exactly equal in measure.

What is the radius of the equation of a circle given below?
$$ \left(x-5\right)^{2} + \left(y-8\right)^{2} = 6^{2} $$

The radius of the given equation is 6 that could also be verified by subjecting the center and radius of a circle calculator.

What is the union of radii all of a circle?

The radii union for a circle is always equal to its center.

Is every chord a diameter?

No, not at all. A diameter passes through the center of the circle. So every diameter is a chord but every chord is not a diameter.

Conclusion:

No doubt the circle equation has nothing to do with area and other parameters, but it also allows you to comprehend various other algebraic domains. Not only this, real life applications are also packed with circle concepts just like estimating the size of planets and any round object. This is where our one and only equation of a circle calculator comes around to assist you to do practical calculations fast enough.

References:

From the source of Wikipedia: Circle, Euclid’s definition, Topological definition, Terminology, Analytic results, Properties, Inscribed angles, Circle of Apollonius

Form the source of Khan Academy: Circle equation review, standard equation, expanded equation

From the source of Lumen Learning: The Circle and the Ellipse, Parts of a Circle, Parts of an Ellipse, Eccentricity, Applications