Statistics Calculators ▶ Empirical Rule Calculator
Adblocker Detected
We always struggled to serve you with the best online calculations, thus, there's a humble request to either disable the AD blocker or go with premium plans to use the AD-Free version for calculators.
Disable your Adblocker and refresh your web page 😊
This empirical rule calculator is an advanced tool to check the normal distribution of data within 3 ranges of standard deviation. Sometimes, this tool is also referred to as a three-sigma rule calculator or the 68 95 and 99.7 rule calculator. Just enter the mean and standard deviation if you select summary data or the sample or population if you select raw data to get the mean values for 68%, 95% and 99.7% of data within 3 SD ranges.
The empirical rule statistics calculator works on the basis of 68 95 99 rule statistics. Well, give a read to this article to know the empirical rule definition, the formula for the empirical rule, and an example of how to use this empirical calculator and empirical rule.
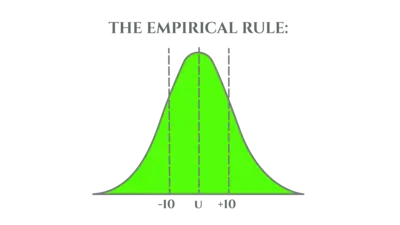
The empirical rule implies that for a normal distribution almost all data lies within 3 standard deviations of the mean. According to this 68 95 99 rule, 68% of the data lies within the first standard deviation. Ninety-five percent of the data is to be kept within second standard deviations. While 99.7% of the data lies within third standard deviations. Empirical rule stats are briefly described as follows:
While you’re dealing with a usual cattering of data, you can use this normal distribution empirical rule because of its ability to estimate probabilities. The empirical rule graph exhibits the three categories of the rule which are shown below:
From the given algorithm you will come to know about the formula, our empirical rule formula calculator also uses the same formula to calculate the normal distribution of data within 3 ranges of standard deviation.
Calculate the mean using: μ = (Σ xi) / n
Find the standard deviation using: σ = √ (∑ (xi – µ) ² / (n – 1))
The empirical rule formula is as follows:
To get the intervals all you have to do is to substitute the values of mean and standard deviation into this calculator for empirical rule.
Empirical Rule is categorized into three percentages, 68, 95, and 99.7. therefore, it is also known as the 68 95 and 99.7 rule.
Different categories of the rule are:
This empirical rule calculator with graph supports you to find out if any specific data follows a normal distribution by checking if 68% of data fall within first standard deviation (σ), 95% of data fall within second standard deviation (σ) and 99.7% of data fall within first 3 standard deviations (σ). Whereas standard deviation, mean and normal distribution are empirical rule statistics.
The whole calculation follows the empirical rule for normal distribution.
Our empirical rule formula calculator has two options, input, and the results. In the input section, there are two choices for the calculation form: (i) summary data and (ii) raw data. If you have the calculated mean and standard deviation, then you should select the first option (summary data). If you have not calculated the mean and standard deviation for your data, then select the second option (raw data). In the case of raw data, you just have to select the sample or population from the drop-down menu and enter the numbers. This tool will automatically apply the statistical empirical rule to give you the values for mean, standard deviation and the percentages of distributions.
If you have summary data, then you must select a ‘summary data’ option. In this case, you have the value of mean and standard deviation for your data. Follow the simple steps to check the data distribution.
Input
Output:
If you have your data in sample or population then you need to select the raw data option from the drop-down menu. The calculator will do the rest.
Input:
Output:
If the values of Standard Deviation and mean are known anyone can calculate the value of empirical rule using empirical rule formula. Down below is the empirical rule example to better understanding the method.
Empirical Rule Formula derivation:
Here;
Example:
Let’s dig a little deep and find empirical rule for the values {12,32,45,53,21,43}
Part 1:
The 1st step is to Calculate Mean
Part 2:
Then find the value for Standard Deviation
This Standard Deviation Calculator can be used to find Standard deviation as well.
Part 3:
The example explained above is to understand the concept of Empirical rule. While doing such tangled calculations on your own, we recommend you to use our empirical rule percentage calculator to verify your results.
The Empirical Rule stats is an estimate that can be used only to those data sets who have a bell-shaped relative frequency histogram. With the help of the empirical rule formula, it calculates the percentage of the measurements that fall within the range of 1, 2, and 3 standard deviations of the mean. Whereas the Chebyshev’s Theorem can be applied to all kinds of data sets even if the data is not normally distributed. It defines the smallest amount of the quantities that fall inside one, two, or more standard deviations of the mean.
Given below are the conditions that are always considered true while applying Empirical Rule Formula:
When it comes to using the symmetry of the bell curve, the percentages may be broken down even further. For instance, the first part of the empirical rule is stated as 68% of the data values are lie within 1 standard deviation. That is from z = -1 to z = +1. You can see that the bell curve (normal distribution) is symmetrical on the right and left, look at the bell curve that half of 68%, or 34%, of the data values lie between z = -1 and z = 0, and the remaining half, 34%, lie from z = 0 to z = +1.
Now, take a look at the second part of the empirical rule.
This part of empirical rule states that 95% of the data values are falls within 2 standard deviations i:e from z = -2 to z = +2. As the bell curve (normal distribution shape) is symmetrical on the right and left, you can notice that half of 95%, or 47.5% of the data values fall from z = -2 to z = 0, while other half that is 47.5% will lie from z = 0 to z = +2. So, by subtracting 34% from 47.5%, you can see that 13.5 of the data values fall from z = -2 to z = -1, while 13.5% of the data values are fall from z = +1 to z = +2. So, it’s time to expand the given diagram with that information.
Now, finally, take a look at the third part of the empirical rule.
The third part of the empirical rule states that 99.7% of the data values are lie within 3 standard deviations i: e from z = -3 to z = +3. While the % of area in the two remaining tails on the right and left should be 4.7%, as 99.7% – 95% is 4.7%. As the bell curve (normal distribution shape) is symmetrical on the left and right, you can note that half of 4.7%, or 2.35%, of the data values fall from z = -3 to z = -2, while the other half, 2.355 will lie from z = 2 to z = 3. So, expand the given diagram for better understanding.
This rule is an evaluation, according to a specific question precisely asks you to explain with the help of this Rule. while representing it you have to draw a normal curve with a line down the in the mid and three to both sides. Now simply write the values from the normal distribution.
Steps to Solving Empirical Rule Questions:
You have to take start with the values of mean, in the second step you have to add standard deviations. It will give you the values to the right. Now minus the standard deviations to get the values to the left. Write the percentages for each section. While doing it manually you have to memorize the values of relevant percentages.
Empirical Rule is also known as 68-95-99.7 rule as according to it for any normal distribution, all of the data will fall within three standard deviations of the mean. Three SD are 68% 95% and 99.7%. this is the reason to call it 69 95 99.7 rule.
If we assume a data set that represents an approximately normal distribution, the values within one standard deviation will be about 68% of the set while about 95% for 2SD and within three standard deviations values will be about 99.7%. in simple words it is a 95% probability.
The rule states that the range is always four times greater than the standard deviation. Whereas the standard deviation is a measure of spread in statistics and plays a significant role in the empirical rule.
It explains the pattern of distribution for any data set from the population. With the support of this rule, if you have only the mean and standard deviation of any normally distributed population, you will be able to calculate the chance or possibility of certain data occurring.
Empirical research is grounded on experiential and measured occurrences and develops data from real understanding rather than from philosophy or faith. Researchers have to collect a real data. By finding values for mean and standard deviation empirical formula rule will be applied to assess the normal distribution probability.
A Z-score also identified as a standard score. It provides an idea that how is the data point from the mean score. But more precisely it’s a term that explains how many standard deviations less or high then the mean score of any population.
Moreover, we can place it on a normal distribution curve.
It means that 68% of values are less than one standard deviation represented by 1SD, 95% of values are less than two standard deviations represented by 2SD and 99% of values are less than three standard deviations represented by 3SD away from the mean respectively.
According to this rule any normally distributed data, will always fall within three standard deviations of the mean. The rule can be divided into three parts: 68%,95%, and 97.5%.
The Empirical Rule is a calculation for normally distributed data only whereas Chebyshev’s Theorem is that rule which can be easily applicable to all sort of data set. It refers to the least percentage of the measurements that fall within one, two, or more standard deviations of the mean.
The empirical rule originates as the same shape of distribution curves appeared again and again to statisticians. It signifies the normal distribution. So we can conclude that it came from the normal distribution.
The normal distribution is a possible distribution of the data. The percentage that falls below the curve within the two points on a distribution graph always points out the possibility that specific value will fall in that interval.
Manual calculations are always chaotic. Use this Empirical Rule Calculator as just by entering the values of mean and standard deviation you can easily find the percent of data values. If you don’t have a calculated mean and standard deviation, then enter your sample or population along with the relevant number and hit the calculate button. You will have the precise results. Additionally, you can use it as a learning tool.
From the source of investopedia – Understanding the Empirical Rule – By WILL KENTON – Example of The Empirical Rule
A Wiley Brand – Form dummies – Employing the Empirical Rule in Statistical Problems – Statistics Problems
From the source of sciencedirect – empirical rule statistics – Explore More By – Sheldon M. Ross, in Introductory Statistics (Third Edition) – Using Statistics to Summarize Data Sets – DESCRIPTIVE STATISTICS – By Sheldon M. Ross, in Introduction to Probability and Statistics for Engineers and Scientists (Fourth Edition)
By wikihow – Co-authored by wikiHow Staff – How to Use the Empirical Rule – Education and Communications – Studying – Subjects – Mathematics
Everybody needs a calculator at some point, get the ease of calculating anything from the source of calculator-online.net. Feel free to contact us at your convenience!
