Margin of Error Calculator

Calculating margin of error becomes easy with the ease of our statistic tool known as statistics margin of error calculator. The tool helps to calculate margin of error based on the Confidence Level (α), Proportion Percentage (p), Sample Size (n), and Population size (N).

Well, give a read to this post to learn about how to find margin of error, the margin of error formula, and much more! So, let’s start with the basic term of the margin of error definition!

What Is Margin of Error (Statistics)?

A margin of error (MOE) is a statistical measurement of the difference between survey results and the population value, expressed as a percentage. In simple words, a MOE tells how many percentages points your results will differ from the real population value. For instance, a 95% confidence interval with a 4 percent margin of error indicates that your statistic will be within 4% points of the real population value 95% of the time.

According to the technical term, the margin of error is said to be as the range of values below and above the sample statistic in a confidence interval. Simply, the confidence interval (α) is a way to reveal what the uncertainty is with certain statistics (that is from a poll or survey). Sometimes margin of error is also known as confidence interval! So, if you seeking the way to find the margin of error for a confidence interval, then you ought to use margin of error confidence interval calculator to get instant results!

The Margin of Error Formula:

The formula’s for margin of error statistics are taken into account to find MOE!

MOE = z * √p * (1 – p) / √n

Our smart margin of error calculator also uses the above margin of error equation.

(MOE) Margin of Error (with finite population correction) = z * √p * (1 – p) / √(N – 1) * n / (N – n)

Where:

• MOE indicates the margin of error,
• z indicates the z-score associated with a level of confidence,
• p indicates the sample proportion, expressed as a decimal,
• n indicates the sample size,
• N is the population size

Example Problem:

Calculate margin of error for the probability expectation p = 0.3, confidence interval 95% & the sample size n = 1000?

Solution:

Given Values:

Probability p = 0.3

Confidence level = 95%

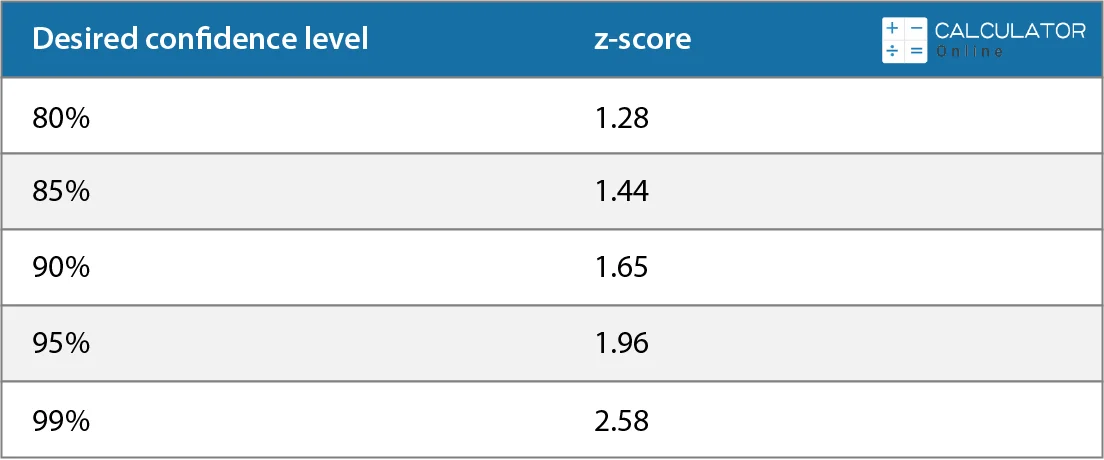
So, the z-score is 1.96 for 95% confidence interval

z = 1.96

Sample size n = 1000

Now, Step by step calculation:

Formula to find ME = z √(p(1-p)/n)

Substitute the values in the above formula

= 1.96 x √(0.3 x 0.7/1000)

ME = 0.028

About Margin of Error Calculator:

Our simple but highly accurate margin of error calculator can help to calculate margin of error of a survey in accordance with the sample size, proportion percentage, population size, and the desired confidence level. You can readily perform the margin of error calculation with this handy tool. Read on!

How to Find Margin of Error With This MOE Calculator:

The tool is very free and simple to use as it is fully loaded with a user-friendly interface, you just need to enter values into the given fields to attain your result! You can compute the MOE within just five simple steps:

• First of all, you ought to select the confidence level from the drop-down menu
• Right after, you have to enter the proportion percentage
• Very next, you ought to enter the sample size
• Then, you have to enter the population size, if required
• Once done, hit the calculate button to generate the MOE value

How to Calculate Margin of Error?

Margin of Error = z * σ/ √n

Where;

n = sample size

σ = population standard deviation

z = z-score

• First, there is a need to get the population standard deviation (σ) and sample size (n)
• Then, there is a need to take the square root of the sample size
• Right after, divide it by the population standard deviation
• Then, there is a need to multiply the result by the z-score consistent with the confidence interval according to the given (z-score) table

FAQ’s:

What is the acceptable margin of error?

Typically, an “acceptable” margin of error will be taken into account by survey researchers that fall between 4% and 8% at the 95% confidence level. You can be able to compute the margin of error at different sample sizes to figure out what sample size will yield results reliable at the desired level.

How do you make the margin of error smaller?

• Increase the sample size
• Reduce variability
• Use a one-sided confidence interval
• Lower the confidence level

What is margin of error in surveys?

The (MOE) is a statistics that expressing the amount of random sampling error in a survey’s outcomes! According to optimistic studies, larger the margin of error, the less confidence one should have that the poll’s/survey reported outcomes are close to the ‘true’ figures that said to be as the figures for the whole population.

What is the purpose of margin of error?

By the definition of margin of error statistics, it is referring to the degree of error in results attained from random sampling surveys. Keep in mind, according to statistic term the higher margin of error referred to as less likelihood of relying on the results of a survey that is the confidence on the outcomes will be lower to represent a population.

What is the margin of error in Slovin’s formula?

Solvin’s formula will be taken into account to calculate the sample size (n) given the population size (N) and margin of error (e). It is determined as n = N (1+Ne2). If a sample is taken from a population, and then a formula should be utilized to take into account confidence levels and margin of error.

Why is margin of error important?

The margin of error around an estimate is immensely important as it assists you to draw conclusions about the data. Remember that a small difference between two estimations may not be statistically significant if the confidence intervals of such both estimates overlap.

How sample size affects margin of error?

Your margin of error assists you to understand whether the sample of your survey is appropriate. If the margin of error looks too big, then you have to increase the size of the sample, in this way the attitudes of the population surveyed match those of the total population more closely.

Final Words:

Enter the values into the above margin of error confidence interval calculator to find (MOE). Maybe you think what you have to do if your answer is inside the margin of error. The only real and best way to reduce the margin of error is to increase your sample size. There is a need to run your survey for a longer period to attain more responses. Good Luck!