Geometric Mean Calculator

This geometric mean calculator helps to calculate the geometric mean for a given set of numbers or percentages. In other words, this calculator allows you to find the geometric average of the statistical set of numbers/percentages.

How to Use This Geometric Mean Calculator?

Finding the geometric mean is very simple, follow the below-mentioned steps to use this geometric means calculator with solution:

• Select whether you want numbers separated by comma or space.
• Enter the set of numbers in the input box.
• Select the number type either numbers or percentages.
• Hit the “Calculate” button.

What is a Geometric Mean?

The number represents the central tendency by taking the nth root of the product of n numbers is referred to as the geometric mean. Also, the geometric average is defined as “the product of n numbers raised to the power of 1/n”. Due to the formula of geometric mean, all the numbers of the data set must have the same sign, they must be all positive or all negative

What is the Geometric Mean Formula?

This online geometric mean solver uses the following formula to find the GM,

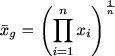
Where,

n is the total number of values

xi is the values of (x1, x2, x3, xn).

This geometric mean equation is equals to,

Geometric Mean for Negative Numbers:

As from the above formula and definition, we can see that we can only calculate the geometric mean for all the positive numbers or the numbers have to be the same sign either manually or by using a geometric mean finder. But this doesn’t mean we cannot find out the geometric mean of negative numbers.

Let’s say we have the changes of production in consecutive three years as 7% growth,9% decline,10%growth. The total growth after three years is 6.89%. But how do we calculate the yearly growth rate?

We can write all the values in proportions as,

• 7% growth = 1+7% = 1+7/100 = 1.07
• 9% decline = 1-9% = 1-9/100 = 0.91
• 10% growth = 1+10% = 1+10/100 = 1.1

Then, the GM = 1.0231

Geometric Mean With Zero

With the below-mentioned tips, you can calculate geometric mean with zero:

• You need to replace any zero with one.
• You can also replace the zero with half of the detection limit.
• Simply add one to each value and then remove that one from the result.

Geometric Mean With Logarithm:

You can also calculate the geometric mean by taking the logarithm of numbers of the data set.

The general formula in terms of logarithm is given below,

log(a*b*c)1/3 = 1/3 * log (a*b*c) = (1/3) * ((log a) + (log b) + (log c)). In simple words, you can find the geometric mean by:

• First, you need to take the logarithm of numbers.
• Calculate the arithmetic mean of the data.
• Then, taking the antilog of the result to find out the geometric mean.

Example to Find Geometric Mean Manually (Step-by-Step)

The formula used for the geometric mean calculation between the numbers is as follow,

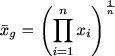
This formula is equivalent to:

Geometric mean example:

Find the geometric mean between 12,23,34?

Solution:

Step 1:

G.M = 3√ (12 × 23 × 34)

Step 2:

G.M = 3√ (9384)

Step 3:

G.M = 21.0926

References:

From the source of Wikipedia: Geometric mean and Calculation, Relationship with logarithms, and much more!

From the source of investopedia: Breaking Down the Geometric Mean in Investing