Compound Inequality Calculator

This inequality calculator solves linear and quadratic inequalities in a smooth way. Solving inequalities has now become just too simple when all the steps are represented in detail.

The step-by-step calculation of the inequalities makes it easy for the students to capture the whole concept of inequality.

The graphical representation of the inequality, whether it is linear or quadratic is also elaborated by the graphing inequalities calculator. The corresponding graph of inequality makes it possible for the students to find the limit of the inequality.

Inequality in Mathematics:

Inequality is a statement of an order greater than, greater than or equal, less than, or less than or equal to between the corresponding numbers or algebraic expressions.

For example:

2 + 4 < 7, 3y – 7 > 8

Operators Used in the Inequality:

The following operators are used to solve inequalities when you are applying the inequalities operations in the compound inequality calculator. You need to understand these operators.

• > Greater than
• >= Greater than equal
• < Less than
• <= Less than and equal 

The inequality values can be represented by the four of the following operators. It is easy to understand the ” >”  Greater than and  “<” Less than. But when we are having >= Greater than equal or <= Less than and equal, then it becomes difficult to understand. It means there are some values where equal values come and at other points, we are getting less than or greater than values.

Rules of  Solving Inequality:

There are certain rules that are followed by the compound inequality calculator when solving inequalities. These rules apply to the inequalities whether it is linear or quadratic inequalities. 

Rule # 01:

When multiplying a negative real number on each side of the inequality, it changes the inequality equations direction. 

This can be understood by the following example:

a>b and c<0. Then a*c<  b*c

Rule # 02:

When multiplying a positive real number on each side of the inequality, It doesn’t change the inequality equation direction. 

This can be understood by the example:

a>b and c>0. Then a*c> b*c.

Rule # 03:

When dividing a negative real number on each side of the inequality, it changes the inequality equation’s direction. 

This can be understood by the example:

a>b and c<0. Then a/c<  b/c. 

Rule # 04:

When dividing a positive real number on each side of the inequality, not change the direction of the inequality equation. 

This can be understood by the example

a>b and c>0. Then a/c>  b/c.

Rule # 05:

Adding the same real number(positive or negative) on each side of the inequality doesn’t have any effect on the direction of the inequality. 

The inequality solver has no effect: 

if a>b  and c R, then a+c>b+c.

Rule # 05:

Subtracting the same real number(positive or negative) on each side of the inequality does have any effect on the direction of the inequality. 

The inequality solver has no effect: 

if a>b  and c R, then a-c>b-c.

Rule # 06:

When Squaring each positive side of the inequality, then it does not affect the direction of the inequality

The inequality is represented as:

0<a<b then a2<b2.

Rule # 07:

When Squaring each of the negative sides of the inequality, then it  does change the direction of the inequality:

 a<b<0 then  a2>b2

Rule # 08:

When Inverting each no zero side of an inequality changes, then  the direction of the inequality:

a<b then 1/a>1/b

You may ask, how do you solve inequalities? So let it be clear that you must try to follow the above-written rules when solving the inequalities. The efficient  inequality solver resolves all the inequalities by implementing the rules of the inequalities.

How to Solve Linear Inequality?

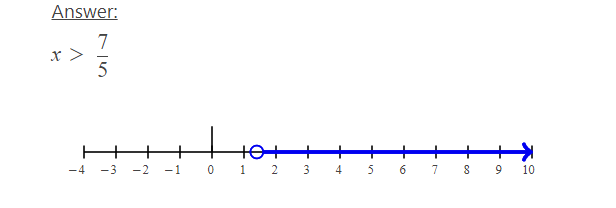
When solving a linear inequality of the type “a.x>b”,then the linear inequalities calculator  is an effective way to solve such inequality. For example when you are entering  an inequality like 5x>7, the linear calculator shows the result like x>7/5 and represents. The graph compound inequality calculator portrays the graphical representation of the simple calculators.

How to Solve a Quadratic Inequality:

When solving quadratic inequality of the form ax2+bx c>0, the process is simple when you have real roots. Quadratic inequalities calculator is quick to respond and all the steps of the inequality are represented step by step. 

When we are putting the x2+6x+9>0 in the compound inequalities calculator, we find the roots x>-3 and  x<3. Both the roots are real in its nature, and when solving and graphing inequalities of the quadratic equation x2+6x+9>0.  The straight line is represented as the graphs lies between values of -3 >x<-3.

Solving the Rational Inequality:

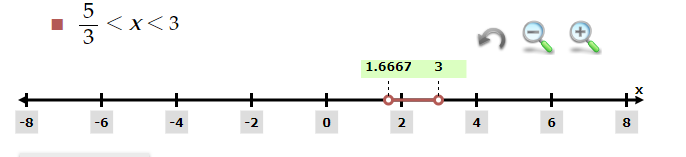
Solving inequalities with fractions of the types (x+1)/(3−x)>2 can be simple and efficient when putting the values in the rational inequality calculator. The compound inequality calculator graph represents the following graph of the rational fraction and solves the following inequality (x+1)/(3−x)>2 in a blink of time too. The answer of the the above mentioned rational fractions is 5/3<x< 3, and  graphical representation is shown below. 

Working of Compound Inequality Calculator:

Solving inequalities by the compound calculator is simple and we have arranged a guide for you people to operate it:

Input:

• From the first drop-down list, go for selecting whether you want to analyze a one sided or compound inequality
• After you do that, go for entering the values in their designated fields
• Also, select the inequality sign from the middle 
• Now if you want to analyze both inequalities at the same time, select “and”, otherwise “or”
• At last, hit the calculate button

Output:

The free calculator does the following calculations:

• The exact result of the inequalities
• Step by step calculations 
• Graphical representation of the answer

References:

From the source of Wikipedia: Properties on the number line, Chained notation, Inequalities between means

From the source of bbc.co.uk/bitesze : inequalities , theorem

From the source tutorme.com: Learning Objective, Introduction, Mathematical Inequality