Cotangent Calculator

The online cotangent calculator finds the value of cotangent by corresponding to the value of a given angle. Also, this cot calculator displays the end result in degrees, radians, m radian, or pi radian as per your requirement. It is functioned to follows the standard cot equation automatically.

Well, keep reading to find the answer of how to find cotangent (cot) and some essential information regarding cot (x).

What is Cot in Math?

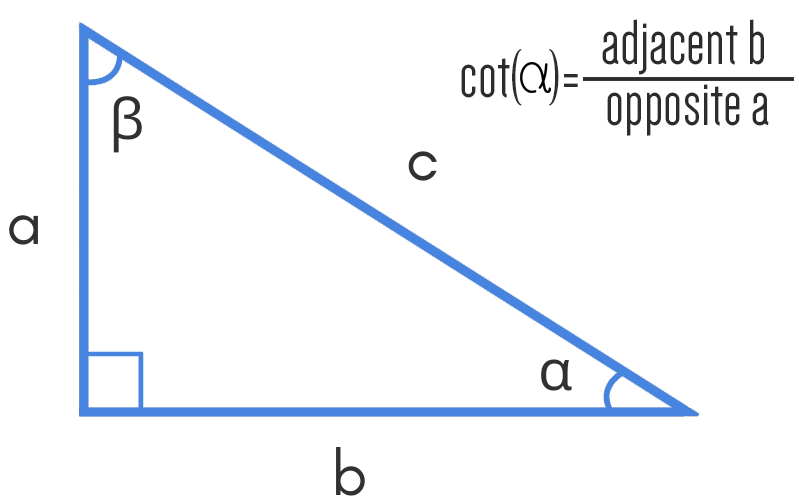
In trigonometry, the cot can be defined as the inverse of the tangent. However, in the case of a right-angle triangle when we divide the length of the adjacent side by the length of the side opposite of the angle then the resulting property is known as cotangent and abbreviated as a cot.

Cotangent is the reciprocal of the tangent:

Cot(x) = 1 / tan(x) = tan(x)-1. Or b / a

However, the cotangent can be represented in the terms of sine(x) and cosine(x).

Cot(x) = cos(x)/sin(x)

Example:

Calculate the cotangent of angle α in a right angle triangle if the length of the adjacent side is 20 and the opposite side is equal to 4.

• Simply put the given values in above mentioned formula: cot(α) = 20 / 4 = 5

Other than that you can also use a cotangent calculator for error-free results.
However, use an Online Tangent Calculator to calculate the tangent values for the given angle in degree, radian, m radian, or the pi (π) radians.

How to Find Cotangent of an Angle?

In a right-angled triangle, the COT of an angle can be figured out by taking the ratio of the adjacent side angle and its opposite angle. However, a COT formula to calculate an angle is:

Cot (α) = adjacent b / opposite a

Instead, a cot calculator might be a good choice to find cotangent of an angle within a fraction of seconds.

Cotangent Table

The following table demonstrates the cotangent values of common angles in radians and degrees. However, all these values can also be calculated by using a cot calculator.

Furthermore, the free Online Arctan Calculator allows you to find the inverse tangent function or arctan (x) in radians, degrees, and different units.

Graph for Cotangent:

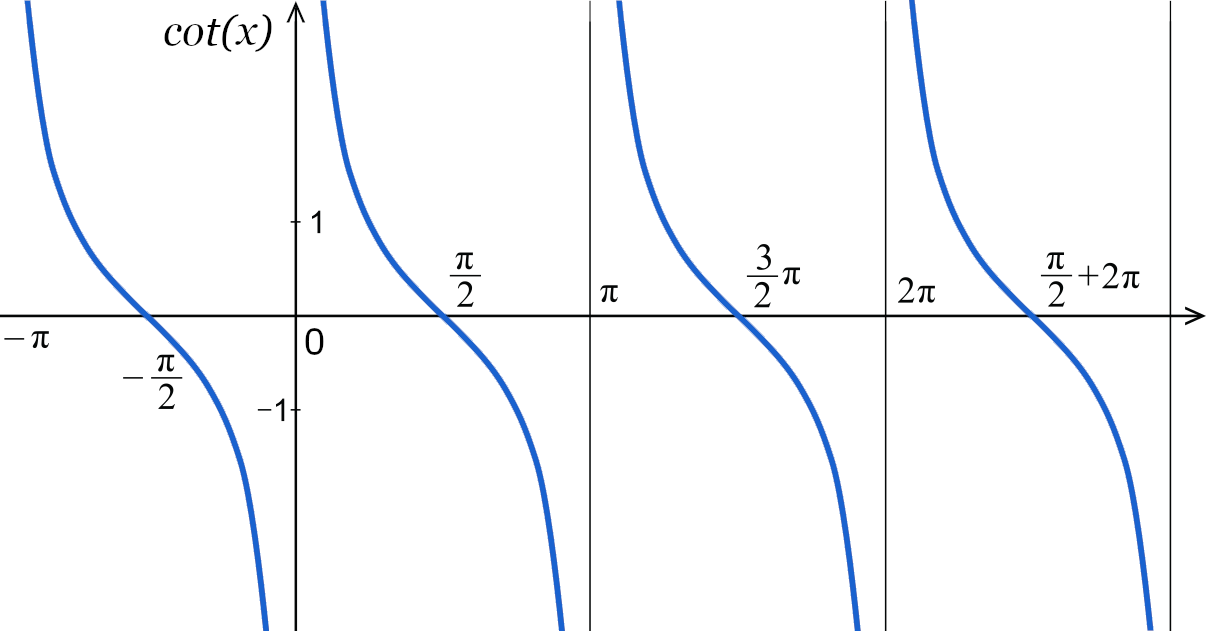
In the form of a graph, the cotangent function for a different angle appears as a series of repeating curves. Additionally, while plotting a graph the key factor to remember is that the cotangent of an angle will never be equal to:

• Zero (0)
• multiple of π radians
• 180°

How Cotangent Calculator Works?

You can calculate cotangent in this calculator in two simple steps:

Input:

• Enter the angle in the given space.
• Now select degrees, radian, M-radian, or pi radian from the drop-down menu.
• Click the “calculate” button.

Output:

Once you enter the angle and unit, the cot calculator shows:

• Value of COT will be displayed either in degrees, radians, M-radian, and pi radian depending on your input field.
• Re-calculate to make another calculation.

Frequently Ask Questions:

How do you Find Cotangent on the Unit Circle?

On a unit circle we can calculate it for an angle by using the x and y coordinates of that specific associated point on the unit circle:

• cot*t=cos*t sin*t=x.y
• t = x . y

However, a cotangent calculator is great support for the calculation of cotangent values for an angle in the blink of an eye. Additionally, if the values of tangent are given the cot-1 calculator will find it as the cot is the inverse of a tangent as well.

What are the 3 Reciprocal Identities?

By the concept of reciprocal identities, statisticians define three reciprocal ratios:

• Cosecant
• Secant
• Cotangent

What is Cotangent used for?

Cotangent can be applied in the same way as sine, cosine, and tangent.  You can use it based on the concept of a right-angled triangle. It can also be used based on the unit circle and in such case, the results angle will be displayed in radians.

What is the Easiest Way to Solve Trigonometry?

Some tips to solve cot trigonometry are:

• Take Start of calculations from the More Complex Side.
• Always prefer to Express everything into Sine and Cosine.
• Apply Pythagorean Identities to convert between sin²x and cos²x.
• Always Know when a right time to Apply Double Angle Formula and addition formula

End Point:

The cotangent calculator helps you to gain knowledge about the cot trig function and its relevant elements. Perhaps, the cot is one of the difficult trigonometric functions, when it comes to manual calculations. Yet, you can still gain mastery of finding the cotangent by using this free online calculator. Opportunely, this is the best option for students and professionals to learn about the cot definition, cot equation calculations as well as related-terms.

Reference:

From the source of Wikipedia: Radians versus degrees, Unit-circle definitions, Algebraic values.

From the source of KhanAcademy: Reciprocal trig ratios, Finding the reciprocal trigonometric ratios, The cotangent (cot).

From the source of Purple Math: Trigonometric Functions and Their Graphs, The Co-Functions, The Cotangent Graph.