Arcsin Calculator to Find Inverse Sine Function with Steps

An online arcsin calculator helps you to calculate the $ arcsin(x) $ or inverse of sine and display the results in radians and degrees. Also, this free inverse sine calculator displays the complete calculation followed by the arcsin formula. However, keep on reading to know about how to calculate arcsine. But, let’s start this context with some basics!

What is arcsin?

In trigonometry, The arcsin function represents the inverse of the sine function. Its purpose is to returns the angle whose sine is a given number.

You can find many devices that consist of the arcsin button or sometimes sin-1 to calculate arcsin.

Every trigonometric function has an inverse function. Such functions always have the same name but the word ‘arc’ will be added as their first name. You can find many devices that consist of the arcsin button or sometimes sin-1 to calculate arcsin. However, the free version of an online sin inverse calculator is the best way to approach trigonometric inverse sin calculations.

Arcsin Formula:

As the arcsine function is the inverse function $y = sin(x)$. therefore, inverse sin equation will be:

$arcsin(y) = sin-1(y) = x + 2kπ$

In this formula $k = {…, -2, -1,0,1, 2,}$.

Every arcsin calculator is functioned to follow this equation as a rule to calculate accurate outcomes.

Example:

For example, if $sin30 = 0.5$ then it is representing that the sine of 30 degrees is 0.5. Therefore, we can say that in this condition arcsin $ 0.5 = 30 $. In other words, the angle whose sin is 0.5 is 30 degrees. You can use the arcsin whenever you know the sine of any particular angle and need to know the actual angle.

How to Calculate Arcsine?

To find arcsin manually all you have to do is to take the equation and put the values in it to have your final outcome. For example, if for example, If the value for sine of $ 30°$ is $0.5$ then what will be the value for arcsin?

So we have $ sin (30°) = 0.5$
Formula for sin inverse is: $arcsin(y) = sin-1(y) = x + 2kπ$
Just put the values: arcsine of 0.5 is 30°: $arcsin(0.5) = sin-1(0.5) = 30°$

However, to avoid the risk of possible errors in this complicated calculation, the use of Arcsin calculator will be a great support.

Similarly, An online arccos calculator helps you to calculate the inverse of the cosine of a given number.

Using Arcsine to find an Angle?

Suppose you have a right-angled triangle. If the known length of side a is $ 52$ and hypotenuse c is $ 60 $ then arcsin can be implemented to figure out the angle $ α $ at point A.

First of all, Calculate the sine of $ α $.
To calculate sine of $ α $, divide the opposite side by the hypotenuse.
$ sin(α) = a / c = 52 / 60 = 0.8$.
now implement the inverse function to calculate the angle $ α $.
$ α = arcsin(0.8666) = 60°$.

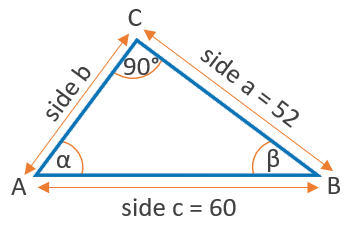
Arcsin Calculator Angle

However, by using an arcsin calculator you can avoid all these steps and have your final outcomes in a matter of seconds.

Table for Arcsin:

Apart from the arc sin formula and calculator, you can also consider the given table that helps you to find some common arc sine values.

The table is given below:

x	arcsin(x) (°)	arcsin(x) (rad.)
-1	-90°	-π/2
-√3 / 2	-60°	-π/3
-√2 / 2	-45°	-π/4
-1/2	-30°	-π/6
0	0°	0
1/2	30°	π/6
√2 / 2	45°	π/4
√3 / 2	60°	π/3
1	90°	π/2

Graph of Arcsin:

Domain, range and other properties of arcsin (x) can be represented on the graph as follows:

arcsin(x) is the inverse function of $ f(x) = sin(x) text{for} – π/2 ≤ x ≤ π/2$
The domain of y = arcsin(x) is equal to the range of $ f(x) = sin(x) text{for} -π/2 ≤ x ≤ π/2$ and can be represented by the interval$ [-1, 1]$ .
The range of arcsin(x) is the domain of f and can be represented by the interval $ [\frac{-π} {2}, \frac{π} {2}]$.

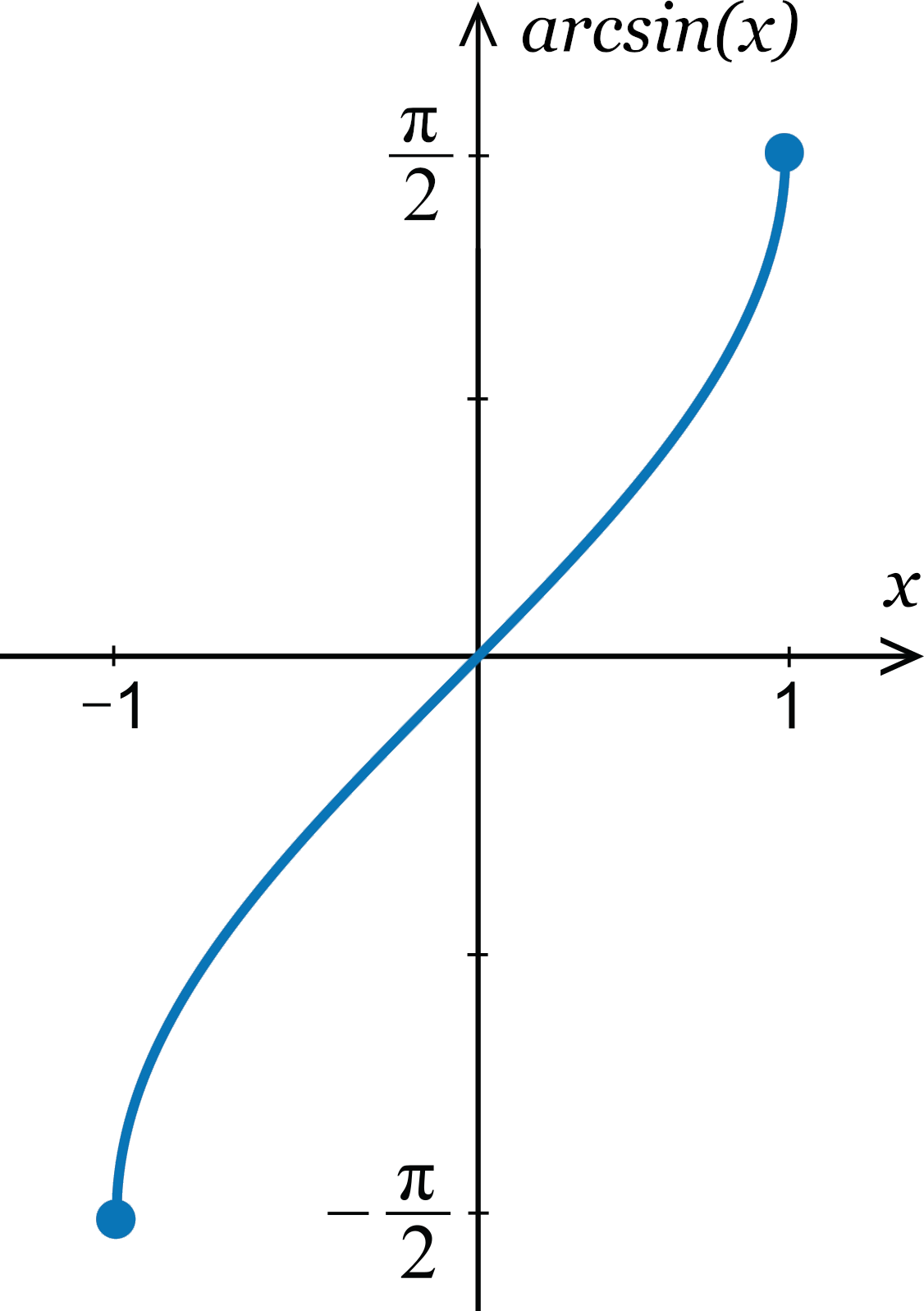
However, the unit circle calculator allows you to determine the different trigonometric values for an angle that helps you to figure out different coordinates of a unit circle.

How Arcsin Calculator Works?

The inverse sine calculator works as follows to find the angle in degrees, radians, and other related units.

Input:

To find inverse sin, you need to enter the value between 1 and -1 in the respective field
Now enter the decimal position. You can select up to 16.
Hit the calculate b button.

Output:

This sin inverse calculator will display:

Angel in radians
Angel in degrees
Result in other relevant units
Complete calculation followed by the equation

FAQs

Is Cosecant the inverse of sine?

Cosecant is the reciprocal of the sine. In a right triangle, It can be expressed as the ratio of the hypotenuse to the side opposite a given angle.

Is Arcsin the same as 1 sin?

$$ sin-1x = arcsin x$$

It means that the arc whose sine is x

What is sin times Arcsin?

To understand it has a look at the following four Arcsin rules:

Sine of arcsine rule is: $ sin( arcsin x ) = x$
Arcsine of sine rule is: $ arcsin( sin x ) = x+2kπ, when k∈ℤ (k is integer)$
Arcsin of negative argument rule is= $arcsin(-x) = – arcsin x$
Complementary angles rules is: $barcsin x = π/2 – arccos x = 90° – arccos x$

How do you calculate arcsine of a unit circle?

With inverse sine, you have to select the angle on the right half of the unit circle that must have measure closes to zero. Therefore, $ sin-1(–½) = –30° or sin–1(–½) = –π/6$ . The range of sin-1 is restricted to $ [–90°, 90°]$.

Endnote:

When it comes to inverse sine calculations, you should hold an arcsin calculator for better and exact results. Therefore, it serves as an exclusive platform for all of those who are keen to acquire knowledge and want to have a strong command of $ arcsin(x) $ function. Furthermore, this inverse sine calculator $ 100%$ free and is equally advantageous for students and educators.

Reference:

From the source of Wikipedia: Notation, Principle Values, Equal identical trigonometric functions.

A source of Math Open Reference: Large and negative angles, Range, and domain of arcsin.

From the source of Mile Foot: Inverse reciprocal identities theorem, Inverse symmetric identities, Inverse cofunction identities theorem.

From the source of Shmoop: Graph of inverse Sine Function, arcsine function.

A source of Brilliant: Inverse trigonometric graphs, domain, and range of inverse sine function.

.tb_button {padding:1px;cursor:pointer;border-right: 1px solid #8b8b8b;border-left: 1px solid #FFF;border-bottom: 1px solid #fff;}.tb_button.hover {borer:2px outset #def; background-color: #f8f8f8 !important;}.ws_toolbar {z-index:100000} .ws_toolbar .ws_tb_btn {cursor:pointer;border:1px solid #555;padding:3px} .tb_highlight{background-color:yellow} .tb_hide {visibility:hidden} .ws_toolbar img {padding:2px;margin:0px}