Law of Sines Calculator

Law of Sines Calculator

Select parameters and fetch their values along with the chosen units. The tool will quickly apply the law of sines to calculate all sides and angles of the triangle

Calculate:

Side a:

cm ▾

Side b:

cm ▾

Side c:

cm ▾

$ A = \sin^{-1} \left[ \dfrac{a \sin B}{b} \right] $

An online law of sines calculator allows you to find the unknown angles and lengths of sides of a triangle. When we dealing with simple and complex trigonometry sin(x) functions, this calculator uses the law of sines formula that helps to find missing sides and angles of a triangle. So, read on to get a complete guide about sine laws.

What is the Law of Sines?

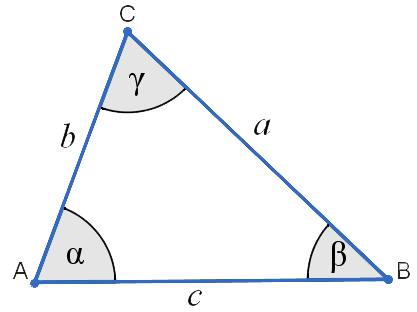
The Laws of sines are the relationship between the angles and sides of a triangle which is defined as the ratio of the length of the side of a triangle to the sine of the opposite angle. Law of Sines Calculator Where: Sides of Triangle: $$a = side a, b = side b, c = side c$$ Angles of Triangle: $$A = angle A, B = angle B, C = angle C$$ Characteristics of Triangle: P = Triangle perimeter, s = semi-perimeter, K = area, r = radius of inscribed circle, R = radius of circumscribed circle If a, b, and c are the length of sides of a triangle and opposite angles are A, B, and C respectively; then law of sins shows: $$a/sinA = b/sinB = c/sinC$$ So, the law of sine calculator can be used to find various angles and sides of a triangle. Example:

Compute the length of sides b and c of the triangle shown below.

Law of Sines Calculator Example Solution: Here, calculate the length of the sides, therefore, use the law of sines in the form of $\frac{a}{sin A} = \frac{b}{sin B}$ Now, $$\frac{a}{sin 100^0}= \frac{12}{sin 50^0}$$ By Cross multiply: $$12 sin 100^0= a sin 50^0$$ Both sides divide by sin $50^0$ $$a = \frac{(12 sin 100^0)}{sin 50^0}$$ From the calculator we get: $$a = 15.427$$ So, the length of sides b and c is $15.427 mm$. However, an Online Sine Calculator will calculate the sine trigonometric functions for the given angle in degree, radian, or the π radians.

Equations Derived from Law of Sines for Angles A, B, and C:

These are some equations that are used by the law of sines calculator which are obtained from the law of sins: $$A=sin^{−1}[\frac{asinB}{b}]$$ $$A=sin^{−1}[\frac{asinC}{c}]$$ $$B=sin^{−1}[\frac{bsinA}{a}]$$ $$B=sin^{−1}[\frac{bsinC}{c}]$$ $$C=sin^{−1}[\frac{csinA}{a}]$$ $$C=sin^{−1}[\frac{csinB}{b}]$$

Derived Equations from Law of Sines Solving for Sides a, b, and c:

In order to find any side of a triangle law of sines calculator fetched some values from law of sines formula: $$a=\frac{bsinA}{sinB}$$ $$a=\frac{csinA}{sinC}$$ $$b=\frac{asinB}{sinA}$$ $$b=\frac{csinB}{sinC}$$ $$c=\frac{asinC}{sinA}$$ $$c=\frac{bsinC}{sinB}$$ Also, you can find alpha (α) by using, $a=n/a, b=n/a, beta (β ) =n/a$ values, while the value of beta is calculated by using $a=n/a, alpha=n/a, b=n/a$.

Ambiguous Case Law of Sines:

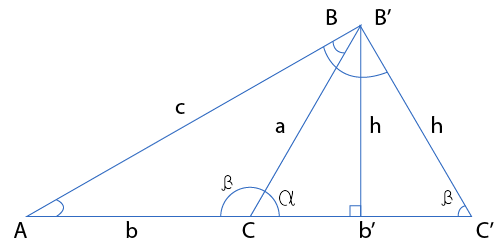
An ambiguous case occurs, when two different triangles constructed from given data then the triangles are $ABC \text{ and} AB’C’$. There are some conditions to use the law of sines for the case to be ambiguous:

When only sin(a)sin(b) and an angle A given.
The angle of A is less than $90^0$.
Side a is shorter as compared to side c.
Side a is longer than altitude h from the angle B where a > h.

Furthermore, The online CSC Calculator will determine the cosecant and sin inverse trigonometric function for the given angle it either in degree, radian, or the pi (π) radians.

How Law of Sines Calculator Works?

The law of sine calculator especially used to solve sine law related missing triangle values by following steps:

Input:

You have to choose an option to find any angle or side of a trinagle from the drop-down list, even the calculator display the equation for the selected option
Now, you need to add the value for angles and sides into the designated fields
Then, you have to select the units for the entered values
At last, make a click on the given calculate button

Output:

The law of sines calculator calculates:

The value of angles and sides for the given equation
The values for the different characteristics of a triangle
Diagram

FAQ’s

When to use the Law of Sines?

When you have two sides and one angle or two angles and one side of a triangle then we use laws of sines.

What is the Main Rule for the Sides of a Triangle?

According to the triangle inequality theorem, the sum of any two sides must be greater than the third side of a triangle and this rule must fulfil all three conditions of sides.

What is Oblique Triangle in Trigonometry?

An oblique triangle is not a right triangle so basic trigonometric ratios do not apply, they can be modified to cover oblique by using sines and cosines law.

What are the Characteristics of a Triangle?

There are different ways to find triangle characteristics:

Radius of circle around triangle $R = (abc) / (4K)$
Radius of inscribed circle in a triangle $r = \sqrt{(s-a)*(s-b)*(s-c) / s}$
Triangle area $K = \sqrt{ s*(s-a)*(s-b)*(s-c)}$
Triangle semi perimeter $s = 0.5 * (a + b + c)$
Perimeter $P = a + b + c$

End-Note:

The law of sines calculator is highly recommendable for assessing the missing values of a triangle by using the law of sines formula. Finding all these values manually is a difficult task, also it increases the risk to get accurate results. By using the law of sine calculator you can find all sine law values instantly and 100% error-free. Moreover, this tool is beneficial for people who work with the law of sine related trigonometric function.

Reference:

From the source of Wikipedia: The ambiguous case of triangle solution, Relation to the circumcircle, Relationship to the area of the triangle. From the source of Dave's Short Trig Course: Oblique Triangles, Pythagorean theorem, Triangle Characteristics. From the source of Khan Academy: Laws of sines and cosines review, Solving triangles using the law of sines, Missing Angle. .tb_button {padding:1px;cursor:pointer;border-right: 1px solid #8b8b8b;border-left: 1px solid #FFF;border-bottom: 1px solid #fff;}.tb_button.hover {borer:2px outset #def; background-color: #f8f8f8 !important;}.ws_toolbar {z-index:100000} .ws_toolbar .ws_tb_btn {cursor:pointer;border:1px solid #555;padding:3px} .tb_highlight{background-color:yellow} .tb_hide {visibility:hidden} .ws_toolbar img {padding:2px;margin:0px}