Parallelogram Calculator

An online parallelogram calculator helps you to calculate each and every parameter of the parallelogram depending upon the set of inputs provided. But before that, you need to go through this context that has been specially arranged to help you people in investigating this geometrical figure.

Give a read!

What Is Parallelogram In Geometry?

“A quadrilateral that has opposite sides parallel to each other is known as parallelogram”

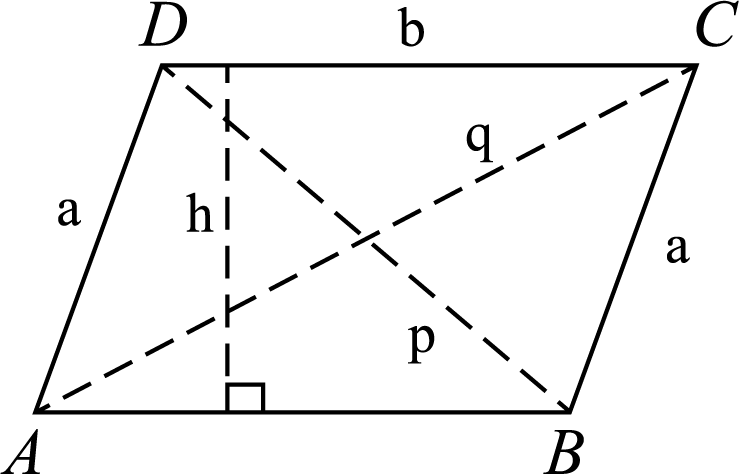
In the above figure:

• a and b are the side lengths (where b is considered the base)
• p and q are the lengths of longer and shorter diagonals, respectively
• h represents the height of the parallelogram
• P and K are perimeter and area, respectively
• A, B, C, and D are the four vertices with respective angles as ∠A, ∠B, ∠C, and ∠D

Parallelogram Important Formulas:

Here we will be discussing all the formulas that are used to determine various technical constants related to parallelogram. These include:

Angles Of Corners:

∠A, ∠B, ∠C, and ∠D are the four angles of the respective vertices A, B, C and D. These angles can be easily determined with the help of parallelogram angle calculator. But you can also determine these angles with the help of the following equations:

$$ ∠A + ∠B = 180^\text{o} $$

$$ ∠A = 180^\text{o} – ∠B $$
$$ ∠B = 180^\text{o} – ∠A $$

Keep the following assumptions in mind:

$$ ∠A = ∠C $$
$$ ∠B = ∠D $$

Point To Ponder:

If the parallelogram is not a square or rectangle, then:

$$ 0 < ∠A < 90^\text{o} \hspace{0.25in} \left(0 < ∠A < \frac{π}{2}\right) $$
$$ 90^\text{o} < ∠B < 180^\text{o} \hspace{0.25in} \left(\frac{π}{2} < ∠B < π\right) $$

Area:

If the angles A and B are given in radians, then you can calculate the area of the parallelogram with the help of the following formula:

$$ K = b * h $$
Or;
$$ K = a*b sin\left(A\right) $$
Or;
$$ K = a*b sin\left(B\right) $$

You can also use the area of a parallelogram calculator to find the area in case you find it difficult to compute manually.

Height:

The height of the parallelogram can be found by using these formulas:

$$ h = a sin\left(A\right) = a sin\left(B\right) $$

You can also make use of the simple-to-use height of a parallelogram calculator to solve for height exactly.

Diagonals:

There are two diagonals in a parallelogram that can be enumerated as follows:

Long Diagonal:

This is the diagonal that is formed by joining vertices A and C.

$$ P = \sqrt{\left(a^{2} + b^{2} – 2ab cos\left(A\right)\right)} = \sqrt{\left(a^{2} + b^{2} +2ab cos\left(B\right)\right)} $$

Short Diagonal:

It is formed by joining the vertices B and D.

$$ q = \sqrt{\left(a^{2} + b^{2} + 2ab cos\left(A\right)\right)} = \sqrt{\left(a^{2} + b^{2} – 2ab cos\left(B\right)\right)} $$\

Also:

$$ p^{2} + q^{2} = 2\left(a^{2} + b^{2}\right) $$

Perimeter Of The Parallelogram:

The following equation can be used to find the perimeter of the parallelogram:

$$ P = 2a + 2b $$

All of these basic limitations can be instantly determined with the help of the free perimeter of parallelogram calculator.

Further Cases(Conversions):

Uptill now, we discussed only basic formulas of the parallelogram. Now, we will be discussing various cases which are based upon the basic formulas mentioned above.

Given the ∠A to determine ∠B, ∠C , and ∠D:

$$ ∠B = 180^\text{o} – ∠A $$
$$ ∠C = ∠A $$
$$ ∠D = ∠B $$

Given the ∠B to calculate ∠A, ∠C, and ∠D :

$$ ∠A = 180^\text{o} – ∠B $$
$$ ∠C = ∠A $$
$$ ∠D = ∠B $$

Given ∠A and a to determine h, ∠B, ∠C, and ∠D:

$$ h = a sin\left(A\right) $$
$$ ∠B = 180^\text{o} – ∠A $$
$$ ∠C = ∠A $$
$$ ∠D = ∠B $$

Given ∠A and h to determine a, ∠B, ∠C, and ∠D:

$$ a = \frac{h}{sin\left(A\right)} $$
$$ ∠B = 180^\text{o} – ∠A $$
$$ ∠C = ∠A $$
$$ ∠D = ∠B $$

Given P and a to calculate b:

$$ b = \frac{\left(P – 2a\right)}{2} $$

Given P and b to calculate a:

$$ a = \frac{\left(P – 2b\right)}{2} $$

Given K and b to calculate h:

$$ h = \frac{K}{b} $$

Given K and h to calculate b:

$$ b = \frac{K}{h} $$

Given b and h to calculate K:

$$ K = bh $$

Given a, b and ∠A to calculate p, q, P, K, h, and ∠B:

$$ P = \sqrt{\left(a^{2} + b^{2} – 2ab cos\left(A\right)\right)} $$
$$ q = \sqrt{\left(a^{2} + b^{2} + 2ab cos\left(A\right)\right)} $$

For the rest of the terms, use formulas discussed above.

Given a, b, and p to calculate ∠A, ∠B, q, h, P, A, and K:

$$ ∠A = arccos\left(\frac{\left(p^{2} – a^{2} – b^{2}\right)}{\left(-2ab\right)}\right) $$

For the remaining parameters, subject to above mentioned equations.

Given a, b, and q to calculate ∠A, ∠B, p, h, P, A, and K:

$$ ∠A = arccos\left(\frac{\left(q^{2} – a^{2} – b^{2}\right)}{\left(2ab\right)}\right) $$

For remaining terms, use formulas already discussed above.

Given a, b, and h to calculate ∠A, ∠B, p, q, P, and K:

$$ ∠A = arcsin\left(\frac{h}{a}\right) $$

Here for the parameters remaining, use formulas that are already mentioned before.

Given a, b, and K to calculate ∠A, ∠B, p, q, h, and P:

$$ ∠A = arcsin\left(\frac{K}{ab}\right) $$

For the rest of the terms, you can make use of formulas already discussed.

Given a, ∠A, and K to calculate ∠A, b, p, q, h, and P:

$$ b = \frac{K}{\left(asin\left(A\right)\right)} $$

Use already mentioned formulas to calculate remaining parameters.

Given a, p, and q to determine ∠A, ∠B, b, h, P, and K:

$$ b = \sqrt{\left(p^{2} + q^{2} -2a^{2}\right)}{2} $$

For other parameters, you can use equations that are already discussed above.

Given b, p, and q to calculate ∠A, ∠B, a, h, P, and K:

$$ a = \sqrt{\left(p^{2} + q^{2} -2b^{2}\right)}{2} $$

And for all terms that are still remaining, you can use the expressions that have already been elaborated above in the context.

Here the area of a parallelogram calculator finds all of these limits with accurate outputs and displays in the form of a well defined table.

How To Solve A Parallelogram?

Finding all the coordinates of a parallelogram may seem a complicated task. But if you understand the most basic equations, you will be able to perform conversions as well. Let us solve a few examples so that you better get the pitch.

Example # 01:

Parallelogram calc: Find P with the following constants given:

$$ a = 2cm $$
$$ b = 4cm $$

Solution:

As we know that:
$$ P = 2a + 2b $$
$$ P = 2*2 + 2*4 $$

$$ P = 4 + 8 $$
$$ P = 12cm^{2} $$

Here the parallelogram perimeter calculator provides with the ease of immediate results whenever you feel a hurdle in your calculations.

Example # 02:

The measure of one angle of a parallelogram is given below:
$$ ∠A = 113^\text{o} $$
Find the remaining angles:

Solution:

We know that:

$$ ∠B = 180^\text{o} – ∠A $$
$$ ∠B = 180^\text{o} – 113^\text{o} $$
$$ ∠B = 67^\text{o} $$

Now converting angle in radians:
$$ ∠B_{rad} = 67^\text{o} * \frac{π}{180} $$
$$ ∠B_{rad} = 67^\text{o} * \frac{3.14}{180} $$
$$ ∠B_{rad} = 67^\text{o} * 0.017 $$
$$ ∠B_{rad} = 1.139rad $$

$$ ∠A = ∠C $$
$$ ∠C = 113^\text{o} $$

Converting In Radians:

$$ ∠C_{rad} = 113^\text{o} * \frac{π}{180} $$

$$ ∠C_{rad} = 113^\text{o} * \frac{3.14}{180} $$

$$ ∠C_{rad} = 113^\text{o} * 0.017 $$

$$ ∠C_{rad} = 1.921 rad $$

$$ ∠B = ∠D $$
$$ ∠D = 67^\text{o} $$

Converting In Radians:

$$ ∠D_{rad} = 67^\text{o} * \frac{π}{180} $$
$$ ∠D_{rad} = 67^\text{o} * \frac{3.14}{180} $$
$$ ∠D_{rad} = 67^\text{o} * 0.017 $$
$$ ∠D_{rad} = 1.139rad $$

Example # 03:

The measure of the height and base of a parallelogram is 4cm and 6cm, respectively. Calculate the area.

Solution:

As we know that:

$$ \text{Area Of The Parallelogram} = b * h $$

$$ \text{Area Of The Parallelogram} = 6cm * 4cm $$

$$ \text{Area Of The Parallelogram} = 24cm^{2} $$

Our free parallelogram area calculator displays the same results but upto more precision and shorter span of time.

Example # 04:

Parallelogram calc: Find a if c the perimeter of a parallelogram is 6.2cm and the measure of the side b is 2cm.

Solution:

We know that:

$$ a = \frac{\left(P – 2b\right)}{2} $$
$$ a = \frac{\left(6.2 – 2*2\right)}{2} $$
$$ a = \frac{\left(6.2 – 2*2\right)}{2} $$
$$ a = \frac{2.2}{2} $$
$$ a = 1.1cm $$

How Parallelogram Calculator Works?

Our free parallelogram solver is the best method considered to thoroughly inspect a parallelogram. If you are indulged in complexity during the calculations and find no way to resolve the problem, then this area of a parallelogram with vertices calculator is a right choice for you. Let us guide you what you need to do:

Input:

• Simply tap “Calculation With” and a drop down list will appear
• Select the parameter with which you wish to find the various related parameters
• Enter the value of the chosen parameters
• Hit the calculate button

Output:

The free diagonal of a parallelogram calculator calculates:

• Sides of the parallelogram
• Angles of the parallelogram
• Diagonals of the parallelogram
• Height of the parallelogram
• Perimeter of the parallelogram
• Area of the parallelogram
• Displays results in the form of table

FAQ’s:

Is parallelogram a rectangle?

No, a parallelogram can never be considered as a rectangle. The reason is that when the angles of the adjacent sides in a rectangle is \(90^\text{o}\), which is not true in case of a parallelogram. This is why a parallelogram can not be considered a rectangle.

What happens if any one of the sides of a parallelogram is changed?

If any one side of a parallelogram is changed, it will not be considered as a parallelogram.

What are different types of quadrilaterals?

Following are various quadrilateral kinds:

• Rectangle
• Square
• Parallelogram
• Trapezium
• Kite
• Rhombus

Conclusion:

Parallelograms are the building blocks of the architect designs. 2D and 3D maps of buildings, houses and huge constructions are designed by using parallelograms. Any wrong calculation corresponding to parameters of the parallelogram will lead towards the destruction of the whole design. That is why an online area of parallelogram calculator is always preferred to carry out computations just beyond the precision.

References:

From the source of Wikipedia: Diagonal, Polygons, Polyhedrons

From the source of khan academy: quadrilateral

From the source of lumen learning: A Bit of Geometry, Similar Triangles