Law of Cosines Calculator

This law of cosines calculator will help you to calculate the sides and angles of a triangle accurately. You can calculate all other remaining sides and measure angles in a triangle by using different forms of cosine law.

What Is The Law of Cosines?

The law of cosines is a collection of formulas that relates the length of sides of a triangle to one of its cosine angles. The cosine law is usually preferred when three sides of a triangle are given for finding any angle A, B, or C of the triangle or the two adjacent sides and one angle is given.

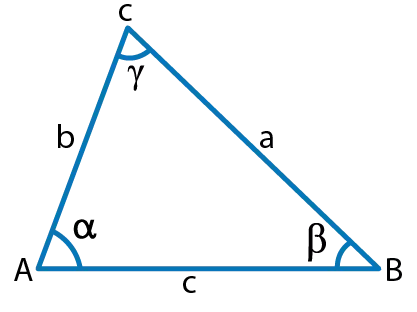
The law of cosines formula is a form of Pythagorean Theorem which adapted for use of non-right triangle, but the Pythagorean Theorem only works for right triangles. So, you can use the law of cosine calculator triangle that applies the law of cosines to find angle and sides in moments.

Law of Cosines Formulas:

If the length of sides is a, b, and c opposite to the angles A, B, and C are given, then the law of cosine expresses:

\(a^2=b^2+c^2−2 \text{ b c } cos(A)\)
\(b^2=a^2+c^2−2 \text{ a c } cos(B)\)
\(c^2=a^2+b^2−2 \text{ a b } cos(C)\)

Law of Cosines For Sides a, b, and c:

In order to find any side of a triangle the law of cosines formula transforms if you know two lengths of sides and the measures of an angle which is opposite to one of them.

\(a=\sqrt{b^2+c^2−2 \text{ b c } cos(A)}\)
\(b=\sqrt{a^2+c^2−2 \text{ a c } cos(B)}\)
\(c=\sqrt{a^2+b^2−2 \text{ a b } cos(C)}\)

Also, if the two lengths of sides and angle are known, then simply add the values into the law of cosines sas calculator, and let it perform calculations.

Law of Cosines For Angles A, B, and C:

If you know three sides of a triangle then you can use the cosine rule to find the angles of a triangle. So, the solving formula for the angles which are used by the law of cosines formula is:

\(A=cos^{−1}[\frac{b^2+c^2−a^2}{2bc}]\)
\(B=cos^{−1}[\frac{a^2+c^2−b^2}{2ac}]\)
\(C=cos^{−1}[\frac{a^2+b^2−c^2}{2ab}]\)

Example:

In triangle (∠ ABC)

• Side a = 9 cm
• Side b = 10 cm
• Side c = 13 cm

Find the largest angle.

Solution:

The largest angle of a triangle is facing the longest side, C:

\(c^2 = a^2 + b^2– 2ab cos C\)

\(cos C = [\frac{a^2+b^2−c^2}{2ab}]\)

\(cos C = [\frac{9^2+10^2−13^2}{2(9)(10)}]\)

\(= 0.067\)

So the largest angle of triangle ABC is

\(C = 86.2^0\)

However, An online Law Of Sines Calculator helps you to find the unknown angles and lengths of sides of a triangle.

How Law of Cosines Calculator Works?

The law of cos calculator helps you to find all unknown missing values of a triangle by using the subsequent steps:

Input:

• First, you need to choose a side or an angle of the triangle that is required from the drop-down menu, then the calculator displays the corresponding form of the law of cosines formula.
• Now, put all the values into a related field.
• Then, select the correlated units.
• After putting all values click the calculate button.

Output:

The law of cosines calculator displays the following results by using the law of cosine formula:

• The measures of all angles and length of sides.
• As well as, the values of different characteristics of the triangle.
• In the end, it draws a diagram for the given values.

Faqs:

What Is The Role of The Pythagorean Theorem In The Law of Cosines?

The law of cosine is a modified version of the Pythagorean Theorem which is used to find unknown values of sides and angles of the non-right triangles.

Is The Law of Cosines Valid Only For Right Triangles?

Not at all! You can easily apply the law of cosines to any kind of triangle without any trouble.

How We Can Prove The Law of Cosines?

We can prove the law of cosine equation by using four different following methods:

• The distance formula
• Trigonometry
• Ptolemy’s theorem
• The Pythagorean Theorem

Reference:

Wikipedia: Ptolemy’s theorem, Obtuse case, Pythagorean theorem, The distance formula.

Versity Tutors: Applications of Law of cosines, The Pythagorean Theorem, Two Sides and the Included Angle-SAS.