Csc Calculator

The online csc calculator will help to find the cosecant (csc) trigonometric function for the given angle it either in degree, radian, or the pi (π) radians. So, if you are especially looking for what is csc in trigonometry, then read through the given context.

Also, here we decided to tell how to find csc trigonometry function, its common value tables, and some basics terms!

What is CSC in Math?

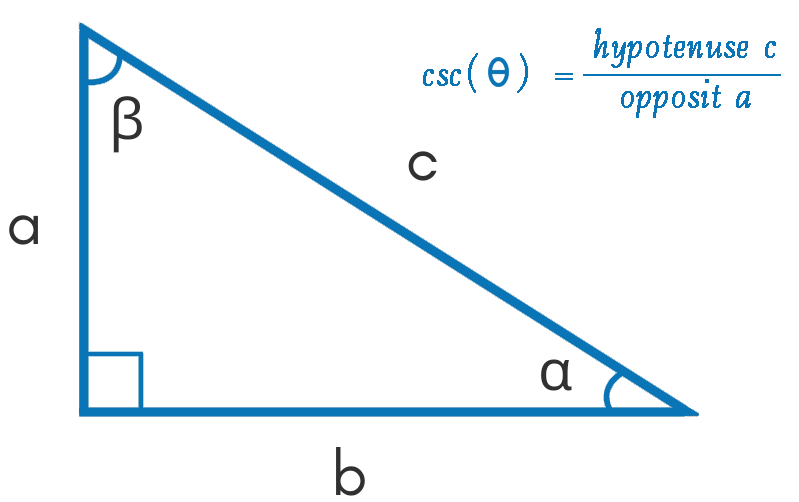
In mathematics, the CSC (cosecant) trigonometry function is the reciprocal of the sine function. When it comes to a right-angled triangle, the csc is referred to as the length of the hypotenuse divided by the length of the side that is opposite of the angle.

Cosecant Formula:

csc θ = hypotenuse / opposite

CSC is equal to:

csc(x) = 1 / sin(x) = sin(x)-1

Well, you could use a simple, but best csc calculator that helps to solve trig function csc (x) quickly.

How to Find Csc of an Angle?

In trigonometry, whenever we want to find the cosecant of angel α in a right triangle, we will apply the csc formula. Furthermore, it can also be defined as the ratio between the angle’s opposite side and the hypotenuse of a right-angled triangle.

Consequently, in simple words above mentioned formula explains that the cosecant of angle θ in any right triangle will be equal to the total length of its hypotenuse c that will be divided by its opposite side a. As well as, take help from a csc calculator for quick and accurate calculation of cosecant of an angel.

However, An Online Secant Calculator assists you to calculate the secant for the given values of a right-angled triangle.

Table for Cosecant:

For quick and rapid calculations that involve some common angles, you can take a look at a cosecant table. It displays the csc values for all the common angles. However, the table is given below:

On the other hand, if you are calculating csc on a calculator then there is no need to memorize the table as it will give you the csc value by using the cosecant formula in the blink of an eye for every entered angel.

Furthermore, An Online Arcsin Calculator helps you to calculate the arcsin(x) and displays the result in radians and degrees.

Graph for Csc:

Whenever the cosecant function for every possible angle drawn on the graph a series of repeating U-curves will be obtained as shown below:

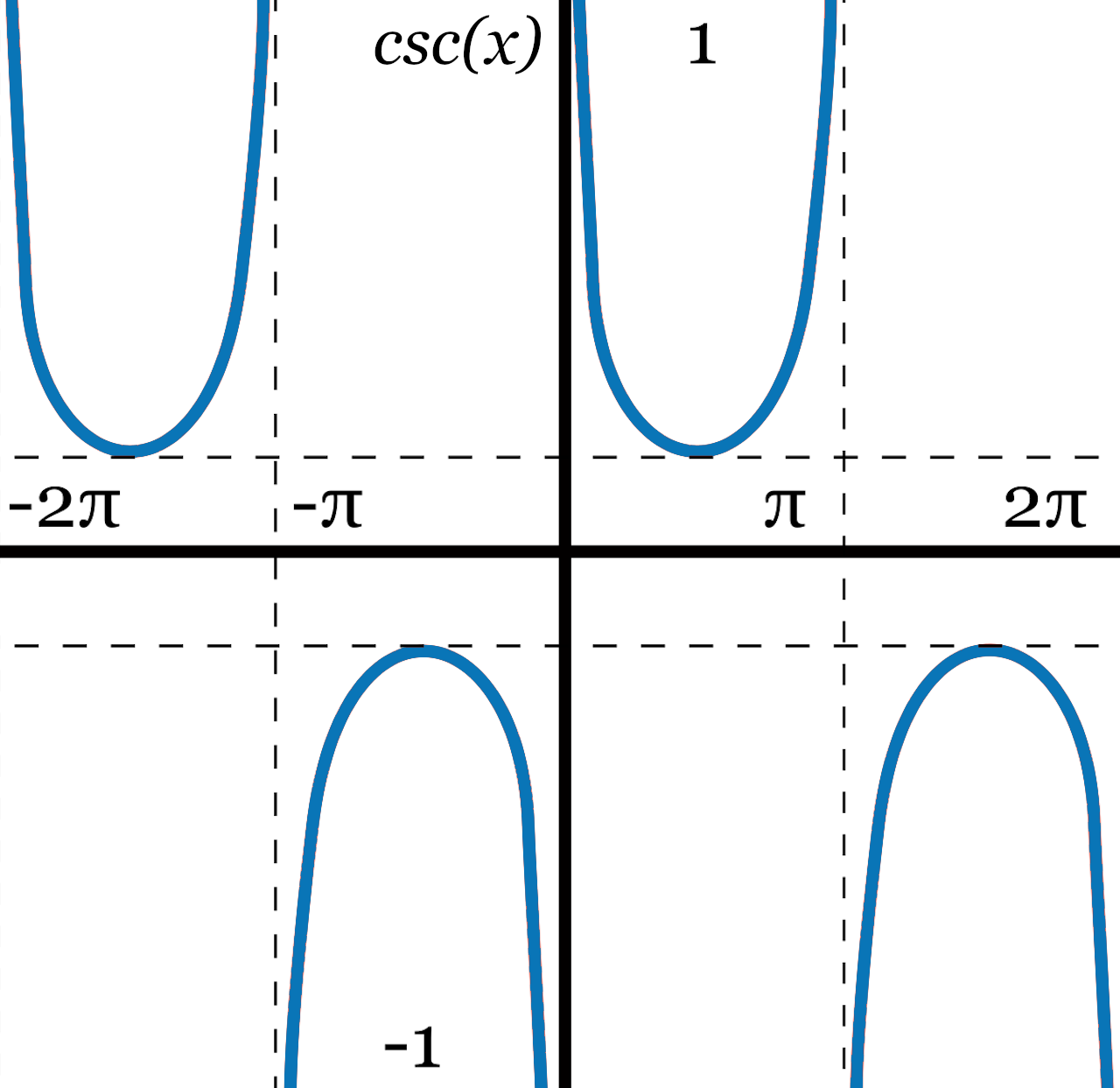
While plotting the graph always keep in mind that the cosecant of an angle will never be in the range of -1 to 1.

There two possibilities:

• It will be greater than or equal to 1.
• It will be lesser than or equal to -1.

Another significant factor to observe is that the curves will never cross the x-axis at an even multiple of π radians, or 180°.

How Csc Calculator Works?

A cosecant calculator will make the most accurate calculations, you need to follow these steps to check your csc trigonometry function:

Input:

• Enter the angel for which you want to calculate cosecant.
• You have to select radian, degree, or π radian from the drop-down menu.
• Click on the calculate button.

Output:

This calculator will follow the csc trig formula automatically and generate the output:

• It will display the value of csc in degrees or radians.
• You can make unlimited calculations by clicking the recalculate button.

FAQs:

How to do CSC on the Unit Circle?

We can use CSC for an angle t by utilizing the y -coordinate of the related point on the unit circle.

• CSC*t=1y *t = 1 y

What are the six basic trigonometric functions?

There are total of 6 trigonometric functions. Out of 6, three are basic and three are derived.

Basic ratios are:

• sine or sin
• cosine or cos
• tangent or tan

Derived ratios are:

• cosecant or csc
• secant or sec
• cotangent or cot

However to calculate cosecant, give a try to csc calculator to have precise results speedily.

What is Trigonometry Formula?

Trigonometry has some Basic Formulas that are given below:

• sin θ = Opposite Side/Hypotenuse.
• cos θ = Adjacent Side/Hypotenuse.
• tan θ = Opposite Side/Adjacent Side.

Who is the Father of Trigonometry?

Hipparchus of Nicaea is considered a father of trigonometry who designed all the basic and derived trigonometry values.

He was also famous as a Greek astronomer, geographer, and mathematician.

Conclude:

You can find different careers that use csc functions to work with the relationships of distances depends on a right-triangle. Well, this is where the term triangulation takes place, so use the above calculator or csc(x) formula to verify your trig calculations!

Reference:

From the source of Wikipedia: Right-angled Triangle, Radians versus Degrees, Algebraic Values.

From the source of CK-12: Cosecant functions, Definition of Cosecant, Formula for find angle.

From the source of Functions Wolfram: Cosecant function, Representation through more general functions, Definition of the cosecant function for a complex argument, Values in points.