Reference Angle Calculator

This reference angle calculator assists you in finding the reference angle that is actually the acute angle display of the given angle in terms of degrees or radians. But before you make use of this free angle measure calculator, let us take you through the article below to understand the basic concept theory of reference angles.

What Is A Reference Angle?

“The smallest measure of the angle that is formed by joining the positive x-axis and the terminal line is known as the reference angle”

Reference Angle Formula:

There arise two cases which are as follows:

Reference Angle In Degrees:

Below are the formulas to find reference angles in degrees:

First Quadrant: \(0^\text{o} - 90^\text{o}\) \(Reference Angle = Angle\)

Second Quadrant: \(90^\text{o} - 180^\text{o}\) \(Reference Angle = 180^\text{o} - Angle\)

Third Quadrant: \(180^\text{o} - 270^\text{o}\) \(Reference Angle= Angle - 180^\text{o}\)

Fourth Quadrant: \(270^\text{o} - 360^\text{o}\) \(Reference Angle = 360^\text{o} - Angle\)

Reference Angle In Radians:

First Quadrant: \(0 - \frac{\pi}{2}\) \(Reference Angle = Angle\)

Second Quadrant: \(\frac{\pi}{2} - \pi\) \(Reference Angle= \pi - Angle\)

Third Quadrant: \(\pi - \frac{3 \pi}{2}\) \(Reference Angle= Angle - \pi\)

Fourth Quadrant: \(\frac{3 \pi}{2} - 2 \pi\) \(Reference Angle= 2 \pi - Angle\)

All of the above-mentioned reference angle formulas are summarized in the following pictorial representation:  

How To Find Reference Angle?

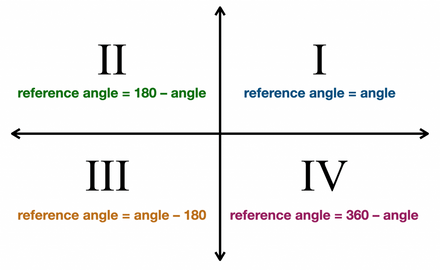
In this section, we will focus on clarifying your concept more precisely by resolving a couple of examples.

Example # 01:

How to find the reference angle of \(43^\text{o}\)?

Solution:

If we recall the angle range for the first quadrant, it is noted that the given angle lies in the first quadrant.

Finding reference angles:

\(Reference Angle = Angle\) \(Reference Angle= 43^\text{o}\)

Which is our required answer.

Example # 02:

How to find the reference angle in radians corresponding to \(43^\text{o}\)?

Solution:

First, we will convert the given angle in radians:

\(Angle In Radians= \text{Angle In Degrees} * \frac{\pi}{180}\)

\(Angle In Radians = (123^\text{o}\)*\(\frac{3.14}{180}\)

\(Angle In Radians = 2.145 rad \)

As the given angle lies in the second quadrant, using the reference angle formula:

\(Reference Angle= \pi - Angle\)

\(Reference Angle = 3.14 - 2.145\)

\(Reference Angle = 0.995 rad\)

How Does the Calculator Work?

Make use of this reference angle finder to find a reference angle in a couple of clicks. Anxious about using this free calculator? Let us go!

Input:

• Write down the angle in the designated field
• From the next drop-down list, select either degrees or radians
• Tap the calculate button

Output: The free standard position calculator calculates:

• Angle in degrees
• Angle in radians
• Angle in \(\pi\) radians
• Displays the graph of the angle in the coordinate system

Reference angles make it possible for you to determine the trigonometric angles that lie outside the first quadrant. Also, you can use these particular angles to find the coordinates of the angles.

References:

From Wikipedia: Angle, Identifying angles, Types of angles, Equivalence angle pairs, Measuring angles, Signed angles, Angles between curves, Bisecting and trisecting angles, Hyperbolic angle From Khan Academy: Trig values of special angles