Tangent Calculator

Use an online tangent calculator to calculate the tangent values for the given angle in degree, radian, m radian, or the pi (π) radians. The trigonometric tan calculator will quickly solve the tangle (α) for the given function.

Additionally, you will get to know about the tangent formula, how to find tangent, its rules, table and graph, and some other relevant terms!

What is Tangent?

Tangent is one of the three trigonometric functions and is abbreviated as “tan”. In a right triangle, the tangent of an angle can be defined as the ratio between the length of the opposite side to the length of the adjacent side. Our tan calculator uses the given tangent formula to find the tangent (x) value.

Tangent Formula:

• Tan formula is: tan(α) = opposite a / adjacent b
• The tangent of angle α can be represented in degree, radian, m radian, or pi radian.

Moreover, the tangent of angle can be defined as sine divided by cosine. So the tangent formula of tan function is defined by

\[tanx=\frac{(sinx)}{(cosx)}\]

Where sin(x) is the sine function and cos(x) is the cosine function.

Furthermore, the Online Free Cosine Calculator helps to calculate the cosine value of the given angle in degrees, radians, mili-radians, and π radians.

Law of Tangents:

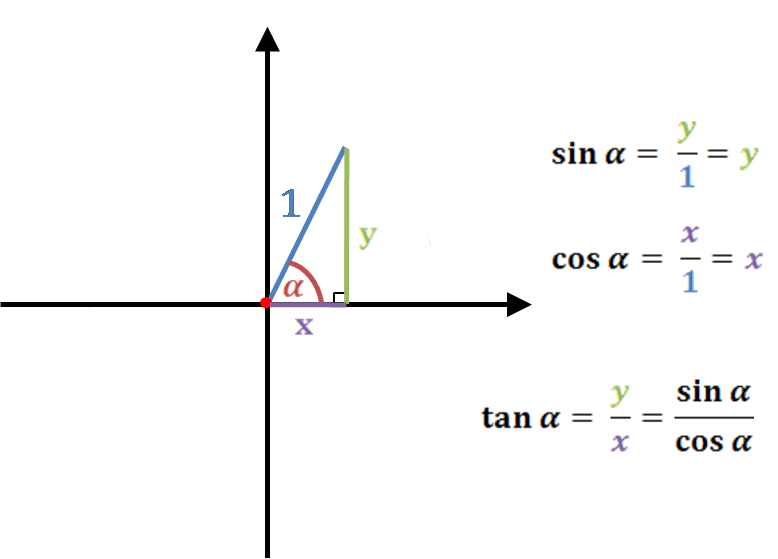
The Law of tangent depicts the relationship between tangents of two angles and opposite side lengths. Then, a right-angled triangle ABC in which sides opposite to ∠A,∠B, and ∠C are a, b,  and c. So, according to the law of tangents, we have the following relation:

$$\frac{a-b}{a+b} = \frac{tan(\frac{1}{2}(a-b))}{tan(\frac{1}{2}(a+b))}$$

However, the free Online Arctan Calculator allows you to solve the inverse tangent function in radians, degrees, and different units.

How to Find Tangent of an Angle?

From the above formula we already know that to find the tangent of an angle we will divide the length of the opposite by the length of an adjacent side. So just put the values in the formula below to find the tangent value of an angel:

\[tan(α) = \frac{a}{b}\]

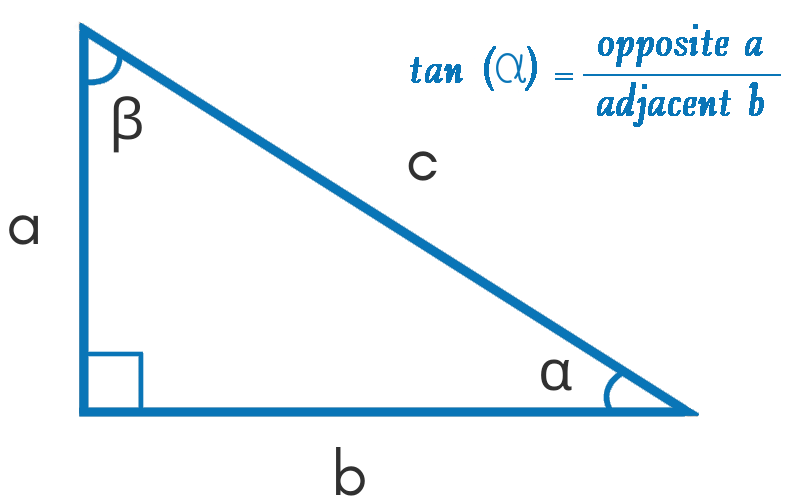
Example:

How to calculate the tangent value of an angel when the length of the opposite side of the angle is equal to 14 and the adjacent side is equal to 7?

Apply the tan equation and put the values:

\[tan(α) = \frac{a}{b}\]

\[=\frac{7}{14}= \frac{1}{2} = 0.5.\]

Though, you can use an online Tangent calculator to calculates the above value of this trigonometric function instantly.

Tangent Graph:

• On graph Tangent function for different angles form multiple curves.
• Curves will start from lower values and moves towards the higher values.
• They will never touch the angles at 90° or 270°.
• A tangent graph will always go between negative and positive Infinity.

Tangent Table:

The following tangent table can be used as a quick reference guide to find the tan value of any angle from zero to 180 degrees respectively.

However, if you want to calculate the tangent value of an angel that is missing in the table then use a tangent calculator. Additionally, an Online Sine Calculator will determine the sine trigonometric values for the given angle in degree, radian, or the π radians.

How Tangent Calculator Works?

A tan calculator will make the most precise calculations, follow these steps to find out your tangent values:

Input:

• Enter the angle for which you want to tangent value.
• Now select radian, degree, m radian, or π radian from the drop-down menu.
• Hit the calculate button.

Output:

This calculator will show the results according to the tangent formula:

• It will display the tangent value for a given angle in degrees or radians (pi or m radian).
• Unlimited calculations can be made by clicking the recalculate button.

FAQs:

How do you solve tan 1?

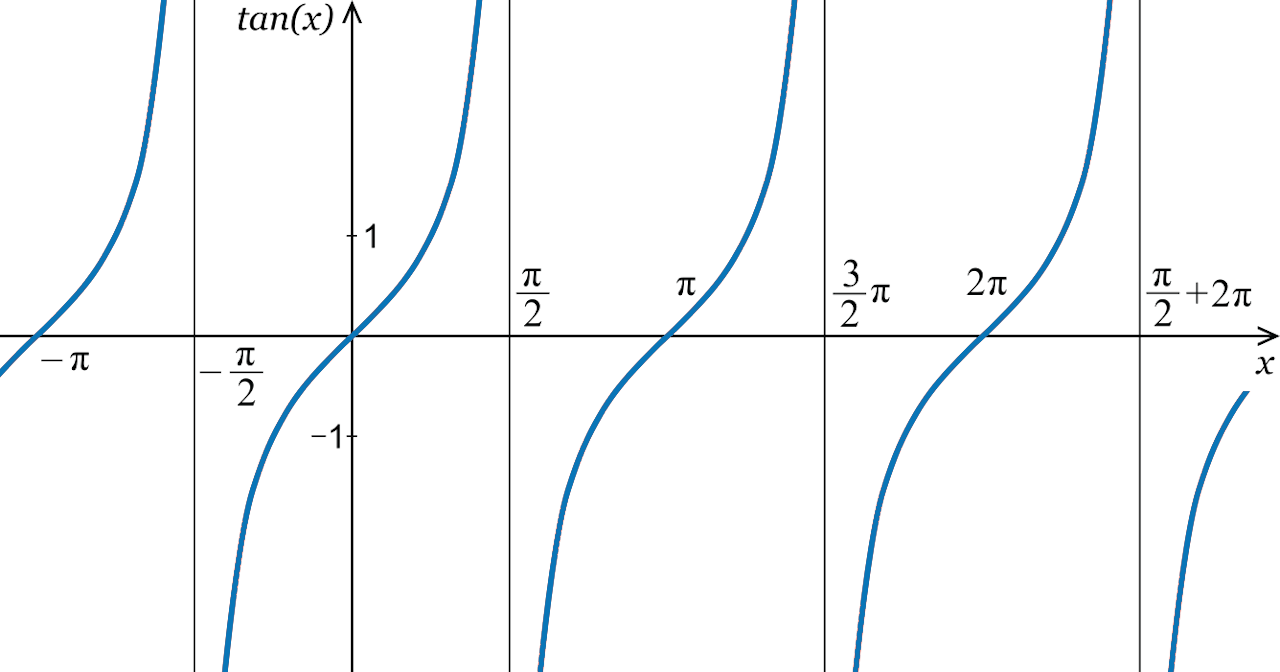
It can be simplified as which angle is equal to tan (-1). In the case of the unit circle tan (1) is equal to pi/4. Meanwhile according to the “Odds and Evens Identity” tan(-x) is equal to -tan(x).

What is Tan Inverse of infinity?

\[Tan 90° = ∞\]

\[Tan π/2 = ∞\]

Therefore,

\[tan-1 (∞) = π/2 or tan-1 (∞) = 90°\]

Does Tan Equal Y X?

According to the definition of unit circle tan(theta) is equals to=\frac{x}{y} or tan(theta)=sin(theta)/cos(theta). The tangent function will be negative every time when sine or cosine, are negative.  However, Tangent is also equivalent to the slope of the terminal side.

What is Tangent in Calculus?

In calculus, a tangent can be defined as the line of the slope of the curve at any specific point. It is the line that will touch the curve at a particular point that has the same direction as the curve.

Conclusion:

This tangent calculator will assist you to find the tangent of any angle you want. It is a great help for students as well as professionals who are dealing with complex angles and their applications in different fields. This calculator does not demand you to remember the tan formula and values for a common angle for quick calculations.

Reference:

From the source of Wikipedia: Right-angled triangle, Algebraic values, Definition by differential equations.

From the source of Libre Text: Power series expansion, Law of Tangents, sum and difference formulas.

From the Source of Cliff Notes: Tangent Identities, double‐angle identity for tangent, reduction identities for tangent.

Other Languages: Tanjant Hesaplama, Kalkulator Stycznej, Kalkulator Tan, Tangenten Rechner, Tan 計算, Tangens Kalkulačka, Calcul Tangente, Calculadora Tangente, Calcolo Tan, Калькулятор Тангенса.