Gram Schmidt Calculator

The free online Gram Schmidt calculator finds the  Orthonormalized set of vectors by Orthonormal basis of independence vectors. The process looks overwhelmingly difficult to understand at first sight, but you can understand it by finding the Orthonormal basis of the independent vector by the Gram-Schmidt calculator.

The Gram-Schmidt Process:

The Gram-Schmidt process (or procedure) is a sequence of operations that enables us to transform a set of linearly independent vectors into a related set of orthogonal vectors that span around the same plan. It can be convenient for us to implement the Gram-Schmidt process by the gram Schmidt calculator.

The Gram-Schmidt orthogonalization is also known as the Gram-Schmidt process. In which we take the  non-orthogonal set of vectors and construct the orthogonal basis of vectors and find their orthonormal vectors. The orthogonal basis calculator is a simple way to find the  orthonormal vectors of free, independent vectors in three dimensional space.

How does the Gram Schmidt Process Work?

The Gram-Schmidt process (or procedure) is a chain of operation that allows us to transform a set of linear independent vectors into a set of orthonormal vectors that span around the same space of the original vectors. The Gram Schmidt calculator turns the independent set of vectors into the Orthonormal basis in the blink of an eye. 

The Orthonormal Vectors:

The Orthonormal vectors are the same as the normal or the perpendicular vectors in two dimensions or x and y plane. When we are going to find the vectors in the three dimensional plan, then these vectors are called the orthonormal vectors. We need a special orthonormal basis calculator to find the orthonormal vectors.

Consider  a set of vectors:

The original vectors are V1,V2, V3,…Vn. The orthonormal basis vectors are U1,U2,U3,…,Un

So we have:

Original vectors → orthonormal basis vectors

 V1,V2, V3,…Vn→ U1,U2,U3,…,Un

 The original independent Vectors 

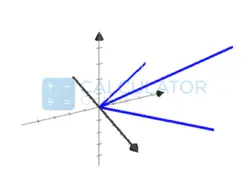
The Orthonormal basis Vectors 

To find the Orthonormal basis vector, follow the steps given as under:

We can Perform the gram schmidt process on the following sequence of vectors:

U1=V1

U2= V2- {(V2,U1)/(|U|1)^2}*U1

U3= V3-  {(V3,U1)/(|U1|)^2}*U1- {(V3,U2)/(|U2|)^2}*U2

Now U1,U2,U3,…,Un are the orthonormal basis vectors of the original vectors  V1,V2, V3,…Vn

Now for Un, we can write:

$$ \vec{u_k} =\vec{v_k} -\sum_{j=1}^{k-1}{\frac{\vec{u_j} .\vec{v_k} }{\vec{u_j}.\vec{u_j} } \vec{u_j} }\ ,\quad \vec{e_k} =\frac{\vec{u_k} }{\|\vec{u_k}\|}$$

You can write the above expression as follows, We can find the orthogonal basis vectors of the original vector by the gram schmidt calculator.

Solved Example:

Consider the following two vector, we perform the gram schmidt process on the following sequence of vectors

$$V_1=\begin{bmatrix}2\\6\\\end{bmatrix}\,V_1 =\begin{bmatrix}4\\8\\\end{bmatrix}$$

By the simple formula we can measure the projection of the vectors

$$ \ \vec{u_k} = \vec{v_k} – \Sigma_{j-1}^\text{k-1} \ proj_\vec{u_j} \ (\vec{v_k}) \ \text{where} \ proj_\vec{uj} \  (\vec{v_k}) = \frac{ \vec{u_j} \cdot \vec{v_k}}{|{\vec{u_j}}|^2} \vec{u_j} \} $$

Step 1:

$$ \vec{u_1} = \vec{v_1} = \begin{bmatrix} 2 \\6 \end{bmatrix} $$

It is simple to calculate the unit vector by the unit vector calculator, and it can be convenient for us.

$$ \vec{u_1} \ = \ \vec{v_1} \  = \ \begin{bmatrix} 0.32 \\ 0.95 \end{bmatrix} $$

Step 2:  

The vector projection calculator can make the whole step of finding the projection just too simple for you.

$$ proj_\vec{u_1} \ (\vec{v_2}) \ = \ \begin{bmatrix} 2.8 \\ 8.4 \end{bmatrix} $$

 The Subtraction of the vectors is :

$$ \vec{u_2} \ = \ \vec{v_2} \ – \  proj_\vec{u_1} \ (\vec{v_2}) \ = \ \begin{bmatrix} 1.2 \\ -0.4 \end{bmatrix} $$

Step 3                                                           

The Final Orthonormal vector is:

$$ \vec{e_2} \ =  \ \frac{\vec{u_2}}{| \vec{u_2 }|} \ = \ \begin{bmatrix} 0.95 \\ -0.32 \end{bmatrix} $$

Working of the Gram Schmidt Calculator:    

Let’s use the Gram Schmidt Process Calculator to find perpendicular or orthonormal vectors in a three dimensional plan.

Input:

• Set the vector size 
• Enter the values of the vectors
• Hit the calculate button

Output:

The Gram Schmidt Calculator readily finds the orthonormal set of vectors of the linear independent vectors.

• The orthonormal set of vectors are displayed
• The steps by step process is represented  

                       

FAQs:

What is a vector?

A vector needs the magnitude and the direction to represent.

What is the main difference between the orthogonal and orthonormal?

The difference between the orthogonal and the orthonormal vectors do involve both the vectors {u,v}, which involve the original vectors and its orthogonal basis vectors. The orthonormal vectors we only define are a series of the orthonormal vectors {u,u} vectors. Where {u,v}=0, and  {u,u}=1, The linear vectors orthonormal vectors can be measured by the  linear algebra calculator.

What is meant by the Orthogonalized matrix? 

A square matrix with a real number is an orthogonalized matrix, if its transpose is equal to the inverse of the matrix. The orthogonal matrix calculator is an especially designed  calculator to find the Orthogonalized matrix.

What is the dot product of vectors?

The (a1.b1) + (a2. b2) + (a3. b3) …. + (an.bn) can be used to find the  dot product for any number of vectors.

What is the condition of Orthogonality?

The two vectors satisfy the condition of the orthogonal if and only if their dot product is zero. The two vectors satisfy the condition of the Orthogonality, if they are perpendicular to each other. It can be convenient to implement the The Gram Schmidt process calculator for measuring the orthonormal vectors.

Conclusion:

In mathematics, especially in linear algebra and numerical analysis, the  Gram–Schmidt process is used to find the orthonormal set of vectors of the independent set of vectors. The gram schmidt calculator implements the Gram–Schmidt process to find the vectors in the Euclidean space Rn equipped with the standard inner product.

References:

From the source of Wikipedia:Gram–Schmidt process,Example

From the source of math.hmc.edu :Gram–Schmidt Method, Definition of the Orthogonal vector