Vector Projection Calculator

Get an instant calculation for projection of one vector onto another vector with this free vector projection calculator. Yes, determining the shadow of a vector on another one is now a couple of clicks away.

So keep in touch with us to understand what basically this physical quantity is and how to measure it by using this free vector projection calculator.

Let’s delve a little bit farther!

What Is The Vector Projection?

In physical terms:

“The length of the shadow that a vector makes over another vector is known as the vector protection”

Vector Projection Formula:

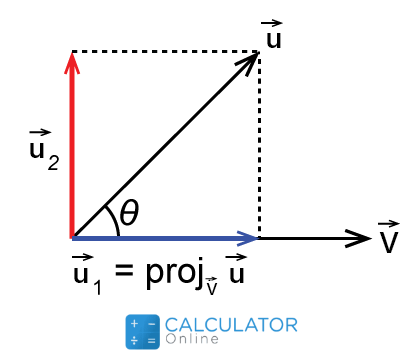
You can easily determine the projection of a vector by using the following formula:

$$ Vector \ Projection=\ proj[\vec u]{\vec{v}} = \frac{ \vec{u} \cdot \vec{v}}{||{\vec{u}}^2||} \vec{v} $$

Our free projection calculator also takes in consideration the above equation to calculate the resultant vector that will throw an outline of its magnitude over the other one.

Scalar Projection:

The scalar resolute of any vector could easily be calculated by using the expression below:

$$ Scalar \ Projection \ | proj[\vec u]{\vec{v}}| = \frac{ \vec{v} \cdot \vec{u}}{|{\vec{u}}|}\ $$

How To Find The Vector Projection?

No doubt this matrix projection calculator vector will generate instant results Get going for getting a firm grip over the concept by having a look at the following examples:

Example # 01:

Find the projection of the vector A over the vector B with the values given as under:

$$ \vecA = 6\veci + 3\vecj + 8\veck $$

$$ \vecB = 3\veci + 7\vecj + 1\veck $$

Solution:

Here we have:

$$ Vector \ Projection=\ proj[\vec u]{\vec{v}} = \frac{ \vec{u} \cdot \vec{v}}{||{\vec{u}}^2||} \vec{v} $$

Determining the dot product of both the vectors:

$$ \vec v.\vec u=47 $$ (For detailed calculations, tap dot product calculator)

Calculating the magnitude of the vector:

$$ |\vec u|=\sqrt{59} $$ (For detailed calculations, tap vector magnitude calculator)

$$ \ proj[\vec u]{\vec{v}}= \frac{47}{\Bigg(\sqrt59\Bigg)^2}.\Bigg(3,7,1\Bigg) $$

$$ \ proj[\vec u]{\vec{v}}= \frac{47}{\Bigg(59\Bigg)}.\Bigg(3,7,1\Bigg) $$

$$ Vector \ Projection \ proj[\vec
u]{\vec{v}}=\Bigg(\frac{141}{59},\frac{329}{59},\frac{47}{59}\Bigg) $$

Which is the required answer and can also be determined by using this vector projection calculator.

How Vector Projection Calculator Works?

Let’s have a look at how this best projection of u onto v calculator will let you calculate the projection of one vector onto the other vector in a blink of moments:

Input:

• First of all, select whether you want to do calculations in the 2D system or 3D system from the first list
• After you do that, you need to select whether you will be selecting coordinates or points for first vector from second drop down list
• Now it’s time to put the values of the first vector in their designated fields
• Repeat the same for the second vector
• Once you are done completely, hit the calculate button

Output:

The best projection vector calculator calculates:

• Vector projection
• Scalar projection

FAQ’s:

What is the projection rule?

Projection law states that:

“If we calculate the sum of the two sides of the triangle made by vector combination, it would actually be equal to the third side”

What is orthogonal projection?

It is the means of displaying 3D objects in space as 2D objects. Being a special form of the parallel projection, it shows lines that are exactly at the right angle to that of the projection plane. This free orthogonal projection calculator will also let you determine such projection of vectors in a blink of moments.

What is the difference between 2D and 3D projection vectors?

2D vectors form a flat image which contains only two coordinates x and y. While on the other hand, the 3D vector introduces another coordinate Z that helps you to go in more depth understanding about the concept.

Why do we use orthographic projection?

Orthographic projection allows you to analyse each and every point drawn in the vector drawing. Moreover, it also assists you in determining the technical information about the vector sheets. And this free orthogonal projection matrix calculator will let you estimate the right angles used in the drawings to reduce error chances.

Conclusion:

Vector projection is a technique in physics that assists you in calculating missing components of the vector in a rectangular coordinate system. It is very handy in simplifying physical concepts like force and work to understand them better. And as far as the fast computations are concerned, this best vector projection calculator will always let you do so without any hurdles.

References:

From the source of Wikipedia: Vector projection, Notation, Scalar projection, Vector projection, Scalar rejection, Vector rejection, Properties

From the source of Khan Academy: Projection of a vector on a line, Dot product

From the source of Lumen Learning: Coordinate Systems, Polar Coordinates, Vectors in Three Dimensions