Power Reducing Formula Calculator

The power reducing formula calculator is a specifically designed trigonometric calculator that is used to reduce and indicate the square, cube, and fourth power trigonometric identities.

The power-reducing identities are used to rewrite the trigonometric angles. It is quickly able to convert the value of the angels sin2θ, cos2θ, and tan2θ  in the highest degrees. The power reducing calculator is reducing the power of the trigonometric ratios to the following power.

• Sin2x, Cos2x, Tan2x
• Sin3x, Cos3x, Tan3x
• Sin4x, Cos4x, Tan4x

What is meant by power reducing:

The power reducing formulas and the procedures are to evaluate the square value of the 3 basic trigonometric ratios. The basic trigonometric ratios are(sin, cos, tan) and we use the power-reducing formula calculator to reduce the value of the identity in the higher units.

In the power reducing formulas, we obtain the second and third versions of sin4θ, cos4θ, and tan4θ. We need to understand the value is going to reduce when we are increasing the power of the trigonometric ratios.

Power reducing formulas:

The most common trig power reducing identities are given below. We need to remember these identities are also used in the power reducing formula calculator.

• sin2θ = [1 – cos (2θ)] / 2
• sin3θ=(sin2θ)(sinθ)

• sin4θ=(sin2θ)^2

• cos2θ = [1 + cos (2θ)] / 2

• cos3θ=(cos2θ)(cosθ)

• cos4θ=(cos2θ)^2

• tan2θ = [1 – cos (2θ)] / [1 + cos (2θ)]

• tan3θ=(tan2θ)(tanθ)

• tan4θ=(tan2θ)^2

Method of reducing the power?

We can understand the concept of the power reducing by the power reducing formula examples:

Example:

Formulate the values of sin2θ, cos2θ, and tan2θ, if the given angle is 30 degrees.

We can find it by putting the values in the sin2θ = [1 – cos (2θ)]/2

Θ = 30

sin2θ = [1 – cos (2θ)]/2

sin2 (30°) = [1 – cos (2(30°))]/2

sin2 (30°) = [1 – cos (60°)]/2

sin2 (30°) = [1 – cos (60°)]/2

sin2 (30°) = (1 – 0.5)/2

sin2 (30°) = 0.5/2

sin2 (30°) = 0.25

As sin3θ=(sin2θ)(sinθ)

sin3 (30°) = 0.125

sin4 (30°) = 0.0625

sin4θ=(sin2θ)^2

The value of cos2θ  in the identity of power reducing formulas [1 + cos (2θ)]/2.

cos2θ = [1 + cos (2θ)]/2

cos2 (30°) = [1 + cos (2(30°))]/2

cos2 (30°) = [1 + cos (60°)]/2

cos2 (30°) = (1 + 0.5)/2

cos2 (30°) = 1.5/2

cos2 (30°) = 0.75

cos 3(30°) = 0.65

As cos3θ=(cos2θ)(cosθ)

cos4(30°) = 0.5625

cos4θ=(cos2θ)^2

The value of tan2θ  in the trigonometric power reduction  [1 – cos (2θ)]/ [1 + cos (2θ)]. We get 

tan2θ = [1 – cos (2θ)]/ [1 + cos (2θ)]

tan2 (30°) = [1 – cos (2(30°)]/ [1 + cos (2(30°)]

tan2 (30°) = [1 – cos (60°)]/ [1 + cos (60°)]

tan2 (30°) = [1 – 0.5]/ [1 + 0.5]

tan2 (30°) = 0.5/ 1.5

tan2 (30°) = 0.33

tan3(30°) = 0.1924

As tan3θ=(tan2θ)(tanθ)

tan4 (30°) = 0.111

tan4θ=(tan2θ)^2

The power-reducing formula calculator can perform all the calculations in the blink of an eye and we can verify all the values by doing the manual calculations.

Working on the power reducing formula calculator:

We can find the values of the trigonometric ratios and their higher power by inserting the value of the angles like 30°,45°, 60°, etc in the trigonometric power reduction calculator. Let’s see how!

Input:

• You can enter the value of the angles.
• Enter the value of the trigonometric ratio to get the angle
• After you are done, hit the calculate button

Output:

The power reducing calculator is used and we are able to find the following outputs.

• We are able to find the value of trigonometric ratios
• The value of the upper value is also shown

FAQs:

What is the value of the cos4x?

For finding the cos(4x), we need to add the values in the cos(4x)=cos(2x+2x)

What are the six trigonometric identities:

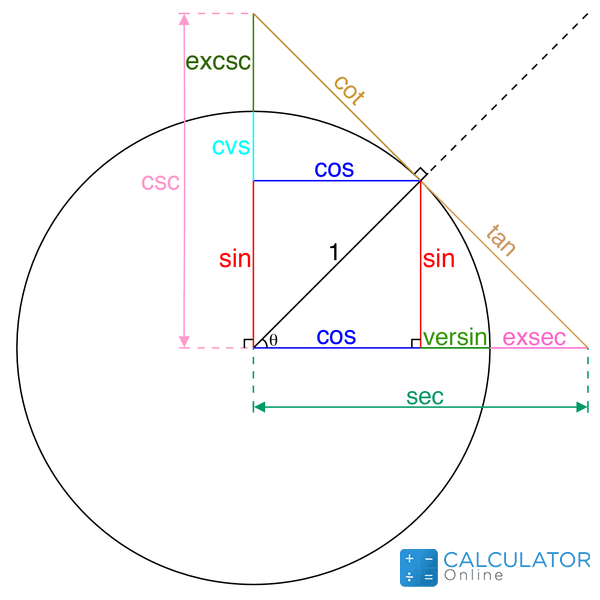
The 6 trigonometric identities are Sine, Cosine, Tangent, Secant, Cosecant and Cotangent. They are written as sin, cos, tan, sec, cosec, and cot.

What are the 3 basic Pythagorean identities in trigonometry?

The 3 Pythagorean identities in trigonometry identities are 

• sin2θ + cos2θ = 1
• sec2θ – tan2θ = 1 
• csc2θ – cot2θ = 1

The final thought:

The power reducing formula calculator is used to find the higher powers of the trigonometric ratios and their values. These values can be used to solve the various numerical problems of calculus.

References:

From the source of Wikipedia: List of trigonometric identities, Pythagorean identities

From the source of clarku.edu:Summary of trigonometric identities, Truly obscure identities.