Change Of Base Formula Calculator

The change of base formula calculator converts one log base value into another. The Change of Base calculator online evaluates the log base values that are not included in the scientific calculator.

Working of Change of Base Formula Calculator:

Get accurate conversions among different log bases with the change of base calculator. It gives you immediate outcomes by inserting a few inputs that include:

Input:

• Enter the values of x, a, and b
• Tap calculate

Output:

• The log base conversion
• Step-by-step calculation

How to Change Base of Log?

You can use the change of base formula to compute the change in the log bases:

The log base change formula is: 

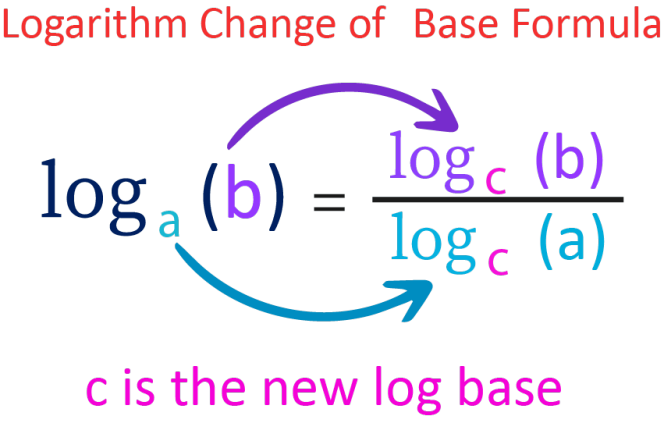
\(log_a(X) = \frac{\log_b(X)}{\log_b(a)}\)

Where:

Log_a =  log with base a

Log_b = log with base b 

The log base conversion is useful when you are finding a log rather than a natural log of base 10 with the scientific calculator 

Practical Example:

Let’s suppose we need to convert the log of base 4 to the log of base 2 for the value X(5). Then how to change the base of the log from 4 to 2.

Given:

Log_a = 4

Log_b = 2

X =  5

Solution:

\(log_ 4(5) = \frac{\log_ 2(5)}{\log_ 2(4)}\)

\(log_ 4(5) = \frac{2.3219}{2}\)

\(log_ 4(5) = {1.161}\)

Get to know the detailed solution of the log of base conversion from one base to another with the  change of base formula calculator

FAQ:

Why Find the Change Base Log?

The change of base is used to find the log of bases 10 and e. The scientific calculator is only going to find the log of 10 and “ln”. You have no option to find a log of bases other than a log of 10 and “ln”. 

How Do I Change the Base of the Logarithm?

If you want to compute log_b(X) given log_a(X), follow these steps:

• Compute log_a(b).
• Divide log_a(x) by the result from Step 1.
• That’s it! The result is log_b(x).

The log base change formula is  log_b(x) = log_a(x) / log_a(b)

Is Log2 the Same as a Natural Log?

No, log2 is a logarithm to base 2, while the base of the natural logarithm is Euler’s number e.

Relationship: log_2(x) = ln x / ln 2

What is the Logarithm of 0?

The logarithm of 0 is undefined. Because, we never get the value 0, by raising any value to the power of anything else.

References:

From the source of Wikipedia: Change of base of log, How to change the base of a log?

From the source of homework.study.com: Convert to log base 10