Radius of a Circle Calculator

Our radius of a circle calculator mainly functions to find the radius of a circle from the values of circumference, area, or diameter.

How Does This Radius of a Circle Calculator Work?

Truly uttering, our calculator is pretty easy to use if you stick to the following usage guide!

Input:

• From the first drop-down list, select the parameter with which you wish to carry the calculations
• After that, enter its value along with the unit selected from the next list
• At last, hit the “Calculate” button

Output:

• Radius, area, diameter, and circumference of the circle

What is the Radius of a Circle?

You all may be familiar with a circle, a well-known and widely used geometrical figure.

“The distance from the center of a circle to any of its points on the circumference is known as the radius”

How to Find the Radius of a Circle?

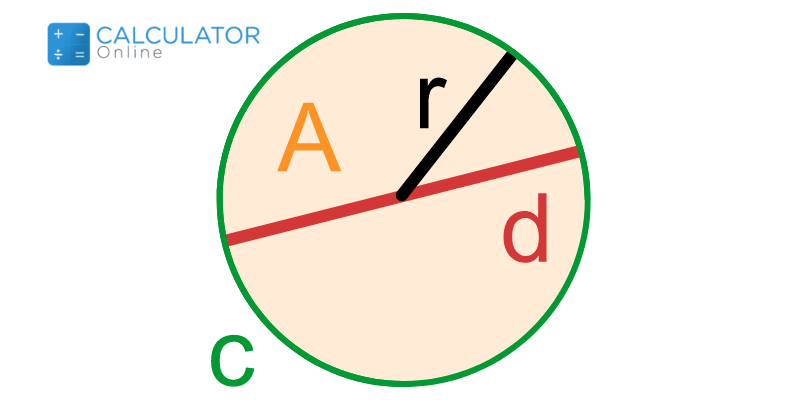
In geometry, a circle is defined by many related entities. And if you are willing to find its radius given different parameters, then these include:

Radius of a Circle Formula:

From Diameter:

As we know that:

\(Diameter=D=2*r\)
or
\(r=\dfrac{D}{2}\)

From Area:

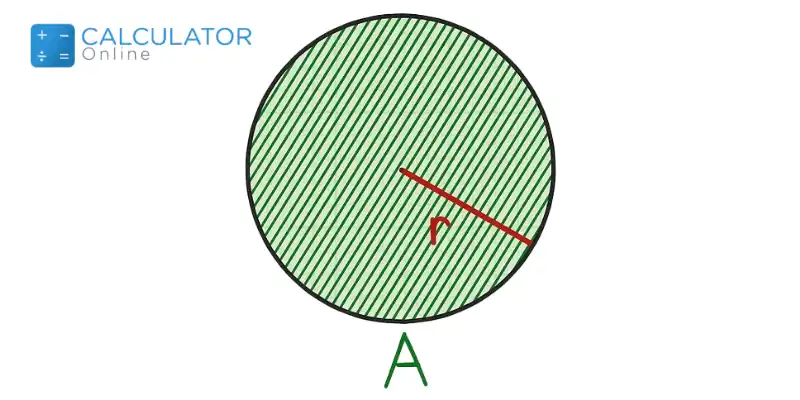
You know that:

\(Area=A=𝜋r^{2}\)
or
\(r^{2}=\dfrac{A}{𝜋})

From Circumference:

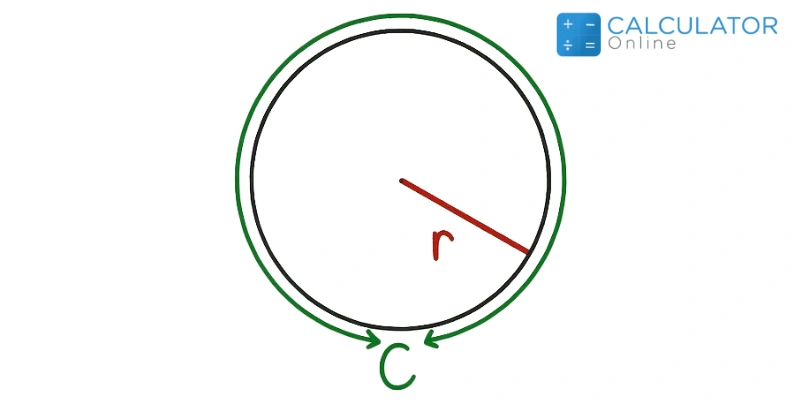
As you know that:

\(C=2*𝜋*r\)
or
(r=\dfrac{C}{2𝜋}\)

From Area and Central Angle of a Sector:

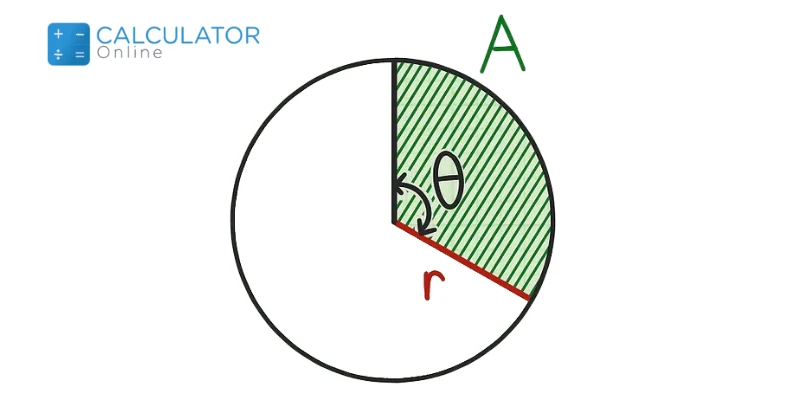
You know that:

\(A=\dfrac{\theta}{360^\text{o}}*𝜋*r^{2}\)
or
\(r=sqrt{\dfrac{A*360^\text{o}}{\theta*𝜋}}\)

Example:

Let us resolve an example that may help you in finding radius of a circle:

Statement:

What’s the radius of a circle having area as \(78m^{2}\)?

Solution:

\(r^{2}=\dfrac{A}{𝜋}\)

\(r^{2}=\dfrac{78}{3.14}\)

\(r^{2}=24.840\)

\(r=\sqrt{24.840}\)

\(r=4.983\)

References:

From the source of Wikipedia: Radius, Formula, Use in coordinate systems

From the source of Khan Academy: Radius, diameter, circumference & π, Labeling, Area of parts of circles

From the source of Lumen Learning: Circles, Equation of a Circle in Standard Form, General form of a circle