Area Between Two Curves Calculator

Use this area between two curves calculator to find the area between two curves on a given interval corresponding to the difference between the definite integrals. In the coordinate plane, the total area is occupied between two curves and the area between curves calculator calculates the area by solving the definite integral between the two different functions.

So, let’s begin to read how to find the area between two curves using definite integration, but first, some basics are the thing you need to consider right now!

What is Area Between Two Curves?

In mathematics, the area between two curves can be calculated with the difference between the definite integral of two points or expressions. In two-dimensional geometry, the area can express with the region covers by the two different curves. There are two functions required to calculate the area, f(x) and g(x) and the integral limits from a to b where b should be greater than $a, b>a$ of the expression.

$Y = f (x) \text{ where x} = a, x = b$

$Y = f (x)$ between limits of a and b

Formula for Area Between Two Curves:

We can find the areas between curves by using its standard formula if we have two different curves

$$m = f (x) & m = g (x)$$

Where

$f (x) \text{ greater than} g (x)$

So the area bounded by two lines$ x = a \text{ and} x = b$ is

$$A = ∫ab[f (x) – g (x)] dx$$

So, the area between two curves calculator computes the area where two curves intersect each other by using this standard formula.

However, an Online Integral Calculator allows you to evaluate the integrals of the functions with respect to the variable involved.

Calculating the Area between Curves:

In order to find the area between two curves here are the simple guidelines:

Need two curves: $y = f (x), \text{ and} y = g (x)$
Find the intersection points of the curves by adding one equation value in another and make an equation that has just one variable.
Solve that given expression and find points of intersection and draw the graph for the given point of intersection and curves.
So the area is $A = ∫ab [f(x)-g(x)] dx$ and put those values in the given formula.
Then solve the definite integration and change the values to get the result.

You can calculate the area and definite integral instantly by putting the expressions in the area between two curves calculator.

Example:

Find area between two curves $x^2 + 4y – x = 0$ where the straight line $x = y$?

Solution:

Given equation is

$$x^2 + 4y – x = 0, x=y$$

$$X^2 + 4y – x = 0$$

Add x and subtract $x^2 $from both sides.

$$X^2 + 4y – x + x – x^2 = x – x^2$$

$$4y = x – x^2$$

Divide by 4 both sides

$$y = x – x^2/4$$

Using another expression where $x = y$ in the given equation of the curve will be

$$X^2+4x-x = 0$$

$$X^2+3x = 0$$

$$X (x+3) = 0$$

Where

$$x = 0 or -3$$

Now, Correlate the values of y, we get $ x = 0 or -3$. So,the points of intersection are $Z(-3,-3) and K(0,0)$. However, the area between two curves calculator provide results by following different points of graph:

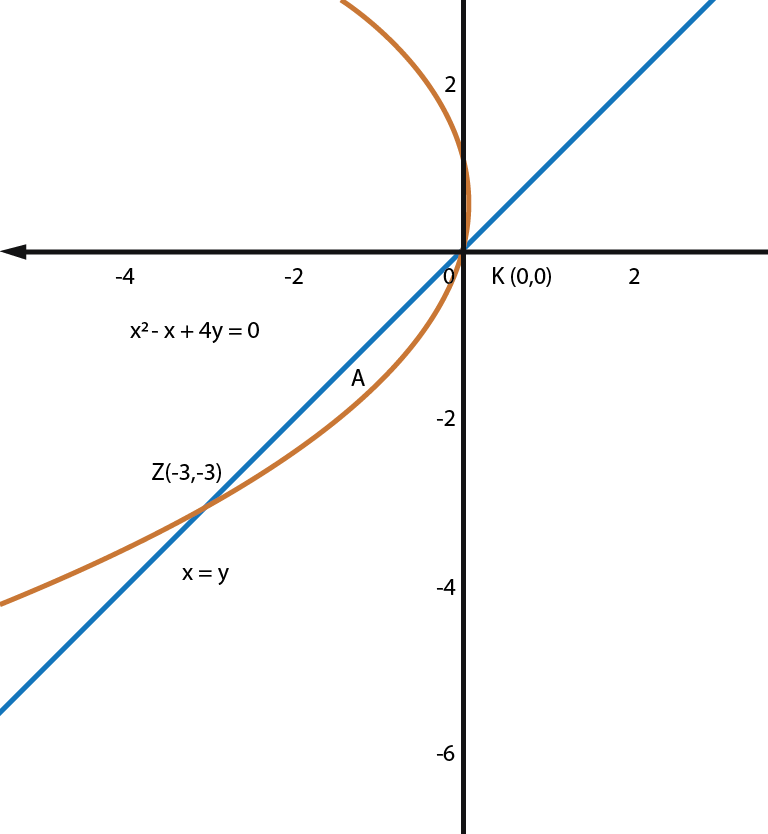
Area Between Two Curves

The graph shows, the curve on the right which is f(x) and the curve on the left is g(x).

$$f(x) = x – x^2/4$$

$$g(x) = x$$

The area is $A = ∫^a_b [f(x) – g(x)]dx$

$$A = ∫30 [(x – x^2/4)-x]dx$$

$$= ∫30 ((-x^2-3x)/4)dx$$

$$= [ – x^3/4*3 – 3/4 * x^2/2]30$$

$$= – [(0+0) – (- 33/4*3 – 3/4 * 32/2)$$

$$= – ( -27/12 + 3/4 * 9/2)$$

$$A= 27/24$$

The area by the definite integral is$ \frac{-27}{24}$.

Furthermore, an Online Derivative Calculator allows you to determine the derivative of the function with respect to a given variable.

How Area Between Two Curves Calculator works?

The area between curves calculator will find the area between curve with the following steps:

Input:

Enter two different expressions of curves with respect to either $x or y$.
Put the definite upper and lower limits for curves
Click on the calculate button for further process.

Output:

The calculator displays the following results for the area between two curves:

Display your input in the form of a proper equation which you put in different corresponding fields.
Shows the area between which bounded by two curves with all too all integral calculation steps.

FAQs for Area between Curves:

Can the Area Between Two Curves be Negative or Not?

If both the curves lie on the x-axis, so the areas between curves will be negative (-). However, the signed value is the final answer.

Why we use Only Definite Integral for Finding the Area Bounded by Curves?

The area between the curves calculator finds the area by different functions only indefinite integrals because indefinite just shows the family of different functions as well as use to find the area between two curves that integrate the difference of the expressions.

What are Definite Integral and Indefinite Integral?

The indefinite integral shows the family of different functions whose derivatives are the f. The differences between the two functions in the family are just a constant. And the definite integral represents the numbers when upper and lower limits are constants.

EndNote:

To find the area between curves without a graph using this handy area between two curves calculator. Basically, the area between the curve signifies the magnitude of the quantity, which is obtained by the product of the quantities signified by the x and y-axis. So, an online area between curves calculator is the best way to signify the magnitude of the quantity exactly.

Reference:

From the source of Wikipedia: Units, Conversions, Non-metric units, Quadrilateral area.

From the source of Brilliant: Area between a curve and the x-axis, Area between a curve and a line, Area between 2 curves.

From the source of Math Online: Areas Between Curves, bottom curve g, top curve f.