Adblocker Detected
We always struggled to serve you with the best online calculations, thus, there's a humble request to either disable the AD blocker or go with premium plans to use the AD-Free version for calculators.
Disable your Adblocker and refresh your web page 😊
How Was Your Calculator Experience? 
We'd Welcome your Feedback
Thank you for visiting our website. You have been selected to participate in a brief customer satisfaction survey to let us know how we can improve your experience
No, Thanks
Table of Content
Our Surface Area Calculator will find the surface area of three-dimensional solids like Capsules, Spheres, Cylinders, Cone, Prism, Pyramids, Hemisphere, Ellipsoid, etc.
We do need to follow the guidelines as under to use the surface area solver.
Input:
Output:
The measure of the total area covered or occupied by an object is known as the surface area of a solid geometrical shape.
A total surface area calculator or different formulas are used for finding the surface area of various solids. The surface area formula has two distinct parts: the base area and the lateral area.
Base area refers to the area of the base of a solid. It can be different for various solids, as it can be rectangular, square, circular, triangular, etc.
The lateral surface is the surface area of all the sides of the solids excluding the base and the top. You can measure the lateral surface area using the lateral surface area calculator.
Below are the surface area formulas for various geometric shapes, have a look at them.
For finding the surface area of the sphere, you need to find the sphere’s radius or its diameter. You can also use a surface area finder to get the radius or diameter.
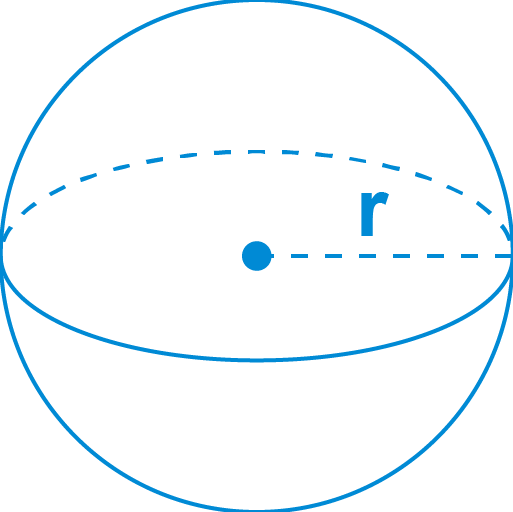
The formula for the surface area of a sphere is:
Where:
r is the radius.
d is the diameter
The surface area of a cone can be measured by summing the base surface area and the lateral surface area. You can also use the surface area of pyramids and cones calculator for more accurate results.
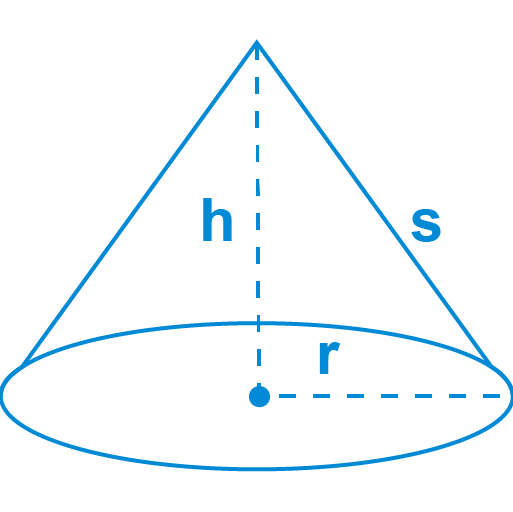
base SA = πr2
lateral SA = πr√r2 + h2
total SA = πr(r + √r2 + h2)
Where
r is the radius and h is the height
The Surface area of a cube can be measured by finding the area of a side and multiplying it by six.
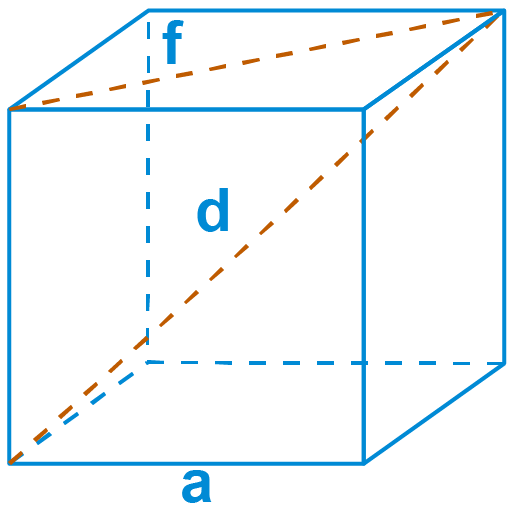
The formula for the Surface area of a cube:
SA = 6a2
Where:
a is the edge length
This formula is also used by the surface area of prism calculator.
The surface area of the cylinder can be measured by summing the base area and the lateral surface area of the cylinder. You can also use the surface area of prism and cylinders calculator to do this task efficiently.
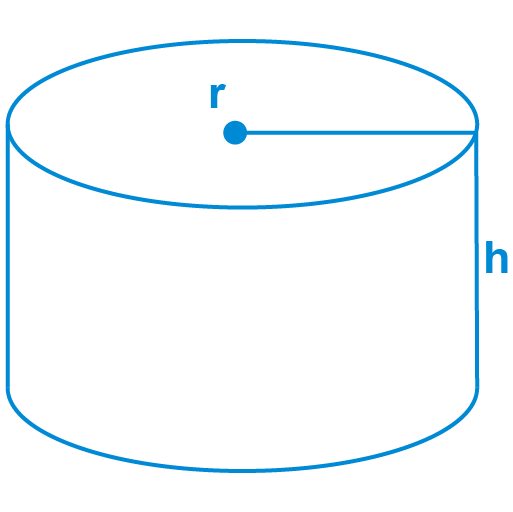
The formula for the Surface area of a cylinder:
base SA = 2πr2
lateral SA = 2πrh
total SA = 2πr(r + h)
where
r is the radius and h is the height
To measure the surface area of a Rectangular Prism, consider the area of three rectangular sides. You can find the area of the Rectangular Prism using the surface area of a rectangle calculator.
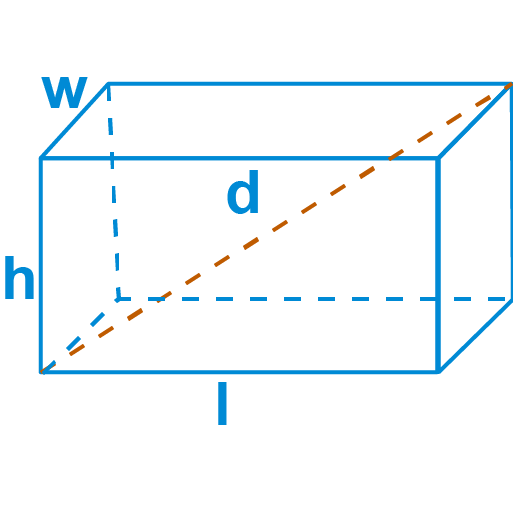
SA of = 2 * (A1 + A2 + A3)
where:
The formula for the Surface area of a cylinder:
A = 2 * (l * w + w * h + l * h)
A capsule surface can be calculated by merging the surface area of the sphere and the lateral surface area of the cylinder.
.png)
The formula for the Surface area of a capsule:
SA = 4πr2 + 2πrh
Where:
r is the radius
h is the height
The surface area of the hemisphere is the curved surface of the hemisphere plus the base area of the circular portion.
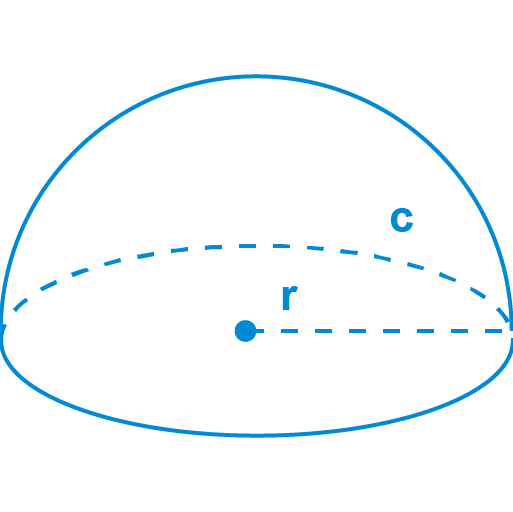
The surface area of the Hemisphere = Curved surface area of hemisphere + circular base area
The curved surface area of the hemisphere = 2πr^2
Circular base area = πr^2
Then
Surface area of the Hemisphere = 2πr^2 + πr^2
Thus,
The surface area of a hemisphere = 3πr^2 square units
Where:
“r” is the radius of the hemisphere.
The surface area of the conical frustum is the sum of two circular portions and the lateral face.
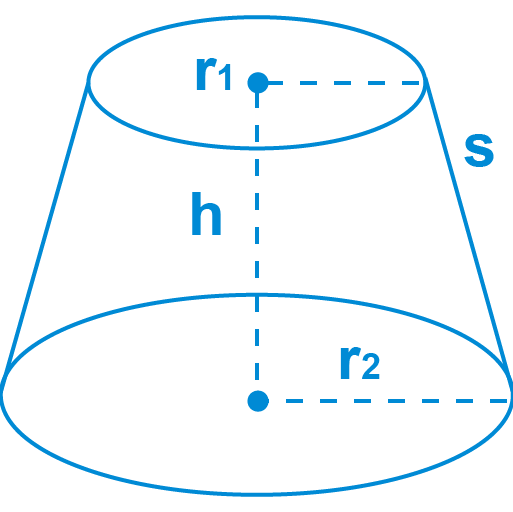
The formula for the Surface area Conical Frustum:
The area of Conical Frustum = Circle Top + Circular Bottom
Circle top = π r2
Circular bottom = π R2
Then
Area of Circular end SA = π(R2 + r2)
lateral SA = π(R+r)√(R-r)2 + h2
total SA = π(R2 + r2) + π(R+r)√(R-r)2 + h2
Where:
R and r are the radii of the ends
h is the height
There are two portions of the Surface area of the Spherical Cap, the spherical cap and the base area. The Spherical Cap includes the height “h” and the area of the circle, and then multiply it by the height.
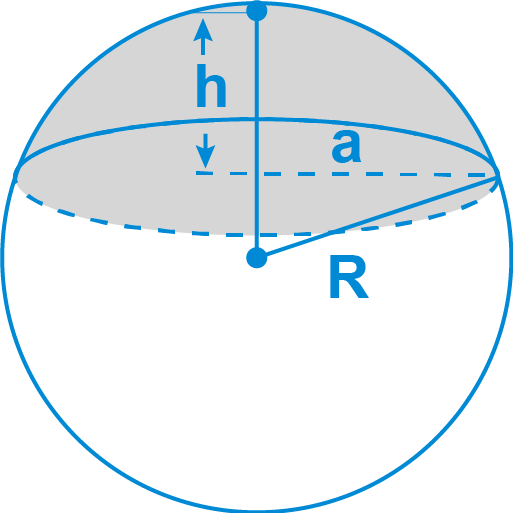
The formula for the Surface area Spherical cap:
Spherical cap SA = 2πRh
Base SA = πr2
SA of Spherical Cap= 2πRh + πr2
The surface area of a Triangular prism can be determined by the perimeter of the face of the Triangular Prism. Now multiply the perimeter by the length and add the base area to it.
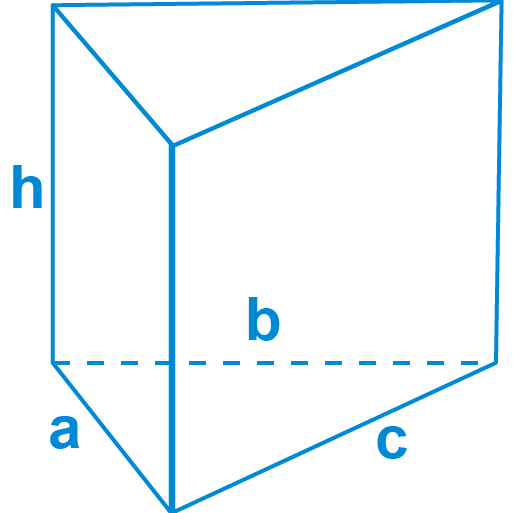
The formula for the Surface area Triangular Prism:
The SA of Triangular prism = (perimeter * length)+ (2 * base area)
The various pyramids can be of different shapes due to their base, the pyramids can be subdivided into various types on the basis of their base shape.
.png)
A = A(base) + A(lateral) = A(base) + 4 * A(lateral face)
In the case of the square base
Lateral Surface Area = a√(a2 + 4h2)
Base Surface Area = a2
Total Surface Area= L + B = a2 + a√(a2 + 4h2))
S.A Pyramid = A(base) + A(lateral) = A(base) + 4 * A(lateral face)
S.A Pyramid = a(a + √(a2 + 4h2))
It can be a little difficult when you are dealing with the various geometrical-shaped pyramids. The surface area of the pyramid can be measured by the surface area of a pyramid calculator
The Ellipsoid Surface area is not simple, you need to learn about the ellipse shape and the vertices.
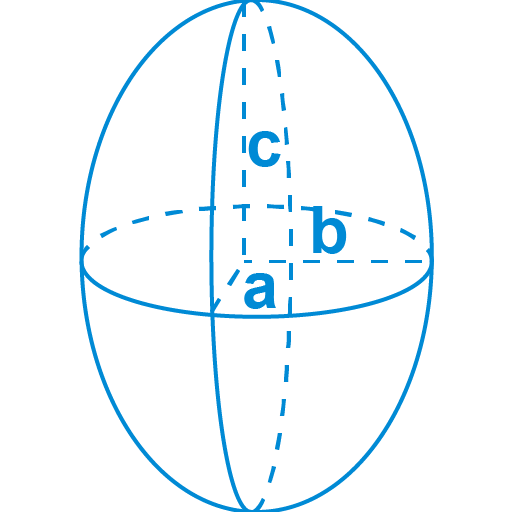
The formula for the Surface area Ellipsoid:
SA ≈ 4π 1.6√(a1.6b1.6 + a1.6c1.6 + b1.6c1.6)/3
where a, b, and c are the axes of the ellipse
From the source of Wikipedia: Surface area,Definition
From the source of the tutorial.math.lamar.edu: Solid Area, Formula of SA
Get the ease of calculating anything from the source of calculator online
Powered By:
Other Website:
Email us at
We are Located at
71-75 Shelton Street, Covent Garden London
Follow Us
© Copyrights 2024 by Calculator-online.net
