Pascal's Triangle Calculator

The Pascal’s triangle calculator generates multiple entries of a specific binomial expansion. It provides important information about the coefficient in a specific row of the binomial series. Pascal's triangle calculator makes it easy to understand the binomial theorem and its expansion. Let's have a look at what is pascal's triangle, and how to use pascal's triangle to make the binomial expansion melaborative.

What is Pascal Triangle?

Pascal's triangle is named after Blaise Pascles, a famous French Mathematician and Philosopher. The Pascal Triangle arrangement makes clear the number of rows(n) and the column(k) such that each number (a) in a given row and column is calculated.

It makes our task much easier and simpler to find the coefficient at a specific place of the binomial series.

Pascal Triangle Formula:

Don’t be too confused with the binomial expansion, as Pascal triangle formula generates critical information. The column notation actually begins with 0, the first value is stored in the first value of the array 0, the second row of the pascal triangle is 1, the third is 2, and so on. The first row is a_1,0, the second is a_1,1, the third number is a_1,2, and so on.

$$ a_{n,k} \equiv \frac{n!}{( k! (n - k)! )} \equiv \binom{n}{k} $$

Where:

n!= The number n value

k!= The number k value

Now k!<= n!

Let's make the task much easier for ourselves, the binomial coefficient calculator is utilized to find the binomial expansion. It provides us with sufficient information regarding the binomial series. The pascal calculations make the task much easier for us, to spot at which point the coefficient is placed.

How to Use Pascal's Triangle?

There are multiple benefits of Pascal’s triangle

• Binomial expansion
• Probability
• Combinatorics

In the binomial expansion of  (a + b)^4, the coefficients of each term are the same for the nth term of Pascal's triangle. Pascal's triangle expansion calculator makes u possible for us t predict future combinations.

Consider an expression (a+b)^4 the coefficient of each term of XY terms are as 1, 4, 6, 4, 1 Pascal's triangle formula for (a+b)^4 is given below:

How to Build Pascal's Triangle?

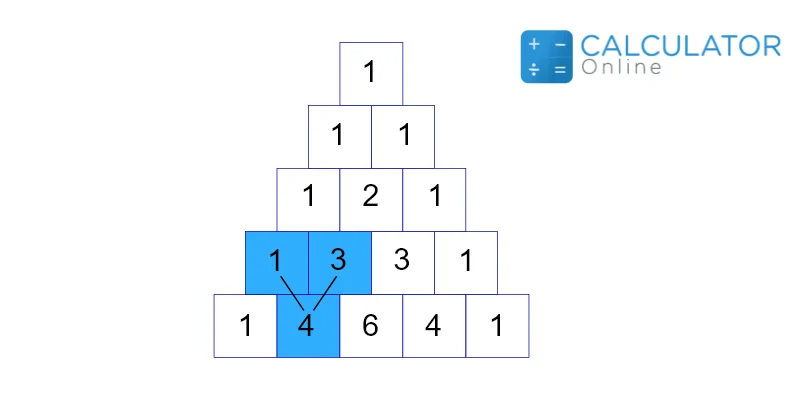
Pascal triangle formula can be generated by the next number in the triangular pattern.

For example, we have highlighted (1+3 = 4), the same we generated (1+2 = 3). For quick retrieval of the expansion, pascal's triangle binomial expansion calculator is responsive and fast. Expand using Pascal's triangle calculator expand, and make the result more resonating for yourself.

Choose the Number of Rows:

Choose the number of rows from the Pascal triangle formula to expand the coefficient with the coefficient. (a + b)^4  has a power equal to “4” starting for 1,4 is:

(a + b)^4 = 1 4 6 4 1

Attach the Coefficient with Pascal's Triangle:

We have coefficient 1 4 6 4 1, attach them with the terms of (a + b)^4 in the same order as the coefficients are appearing in the proceeding order:

(a + b)^4 = 1a + 4ab + 6ab + 4ab + 1b

Place the Power to Coefficient:

Place the power to the variables a and b. Power of a from 4 to 0, and power of b should go from 0 to 4.

(a + b)^4 = 1a^4+ 4a^3b + 6a^2b^2 + 4ab^3+ 1b^2

(a + b)^4 = a^4+ 4a^3b + 6a^2b^2 + 4ab^3+ b^2

We have done the Binomial expansion by the (a + b)^4 using Pascal triangle formula. Pascal’s triangle calculator expand provides us with the values of the binomial expansion in simple steps.

Fibonacci Sequences and Pascal's Triangle Formula:

The Fibonacci Sequence is one of the most difficult sequences to understand. Now with the help of Pascal calculations, it can be easy to understand the sequence.

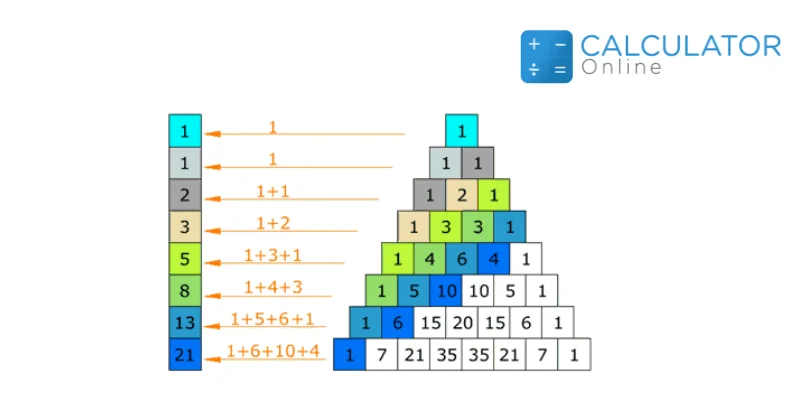
The Fibonacci Sequence starts by “0,1 and then continues by adding the two previous numbers 3+5=8,Pascals triangle row 8, and the next series Fibonacci Sequence number would be  5+8=13, which is the pascal's triangle 13th row. The Pascals triangle calculator makes the Fibonacci Sequence easy to understand.

Table of Pascals Triangle:

Pascal's triangle formula is implemented to find the values in various rows.  Considering Pascal's triangle formula, we have presented the expected values in the table below: the power of the series is actually the row number. The Pascals triangle calculator makes the coefficient of each row easy for us to understand.

The Pascal triangle calculator enable us to predict the coefficient of the even 20th row or 30th row binomial expansion.

Working of Pascal’s Triangle Calculator:

Let's go through the working guide of this free Pascal triangle calculator that lets you calculate the instant results as 

Input:

• Select the option from the list
• Enter the number of rows and columns
• Hit the calculate button 

Output: The result produced by the Pascals triangle calculator is as follows:

• The specific row and its coefficient  
• The pictorial representation displays 

FAQs:

What is the horizontal sum of Pascal's triangle?

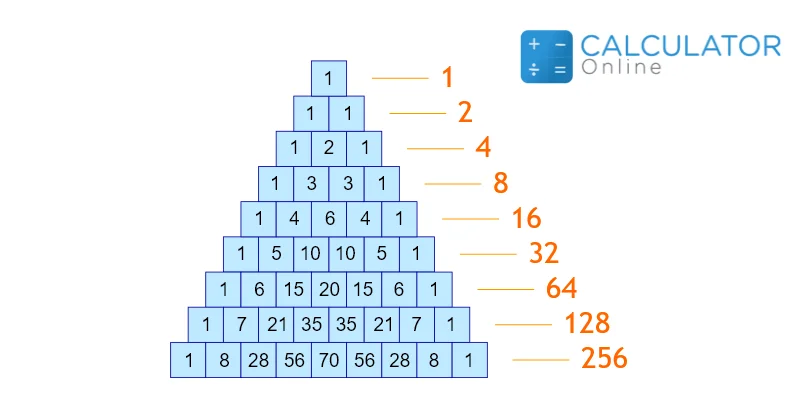
The horizontal sum of all the numbers is doubled each time when we are adding them, so we got the pattern as 1,2,4,8…, and we got the multiple of a power of 2 in all the powers of the 2. Pascal's triangle binomial expansion calculator confirm all the expansion of Pascal's triangle.

Is Pascal's triangle symmetrical?

The triangle is symmetrical, the numbers on the left-hand side have identical matching numbers on the right-hand side like the mirror image. We can expand using Pascal's triangle calculator and can find the same mirror image values.

What is the relation between Pascal's triangle and the exponent of 11?

The exponent of 11 actually represents the number of rows of Pascal's triangle.

• 11^0=1 (the first line is just a "1")
• 11^1=11 (the second line is "1" and "1")

• 11^2=121 (the third line is "1", "2", "1")

Conclusion:

We can predict the coefficient of a specific row and column by the pascal's triangle formula. The Pascal’s triangle calculator makes the task easy for the users, and we can understand the Binomial expansion more explicitly.

References:

From the source of Wikipedia: Pascal's triangle, Formula From the source of Britannica.com: Quiz, Pascal's triangle