Orthocenter Calculator

An online Orthocenter calculator helps you to calculate the orthocenter of a triangle easily. This tool results in exact values of the coordinates of the orthocenter.
Let us discuss the proper concept of the orthocenter in trigonometry.

What is Orthocenter?

“A point where the altitudes of the triangle meet is known as the point of concurrency or simply the orthocenter of the triangle.”

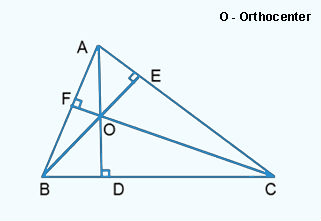
In the above figure, AB, BC and CA are the sides of the triangle and their respective altitudes are CF, AD and BE.

An altitude is simply a perpendicular line (a line drawn at 90 degree angle) that is drawn from any vertex of the triangle to its opposite side. When all right bisectors of a triangle intersect each other at a common point, that point has its own coordinates that are related to the coordinates of all the three vertices of the triangle.

An orthocenter finder generates the absolute values of these coordinates within seconds.

Properties of Orthocenter:

Let us have a focus on some of the significant properties of the orthocenter.

Orthocenter of Acute Triangle:

An acute triangle is the one that has all three angles (acute angles) less than 90°. In general, the orthocenter of an acute-angled triangle lies inside the triangle.

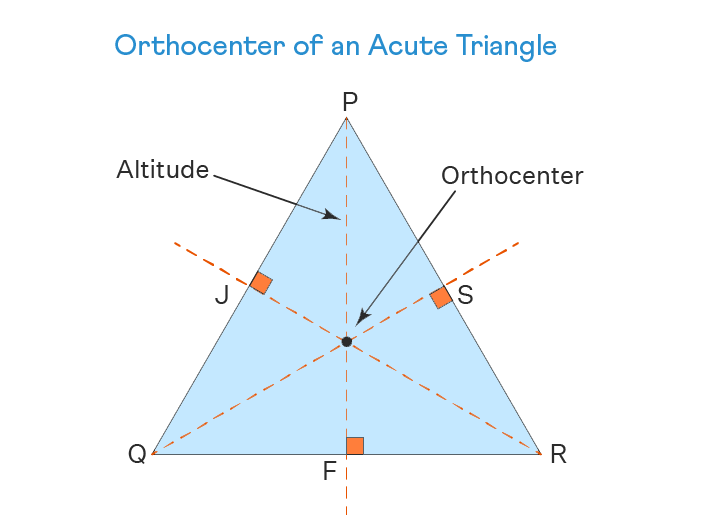
You can determine the orthocenter coordinates by using free online orthocenter calculator.

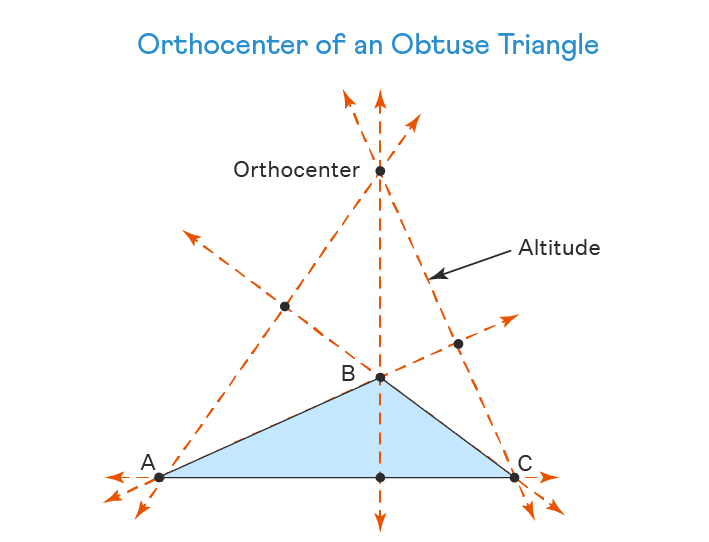
Orthocenter of Obtuse Triangle:

The measure of one angle(obtuse angle) in an obtuse triangle is greater than 90°. For this triangle, the orthocenter always lies outside the triangle.

Orthocenter of Right Triangle:

For a right-angled triangle, the orthocenter lies on its vertex.

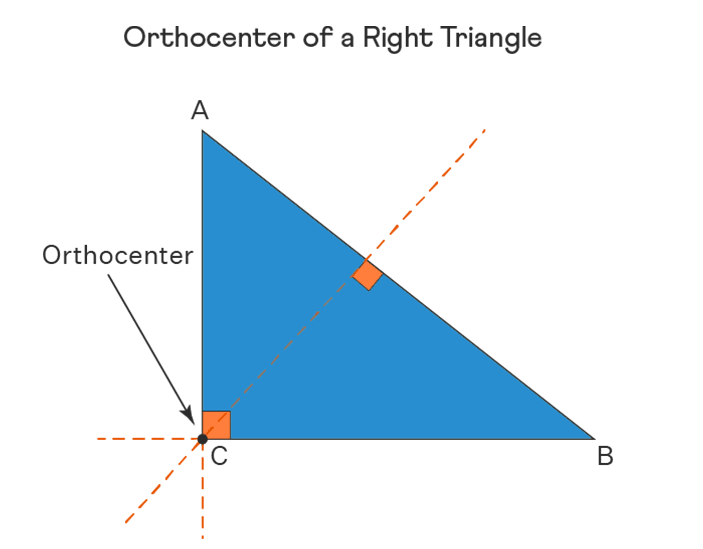
The orthocenter calculator determines the orthocenter of any one of the triangles mentioned above.

Algebraic Formulae to Calculate Orthocenter:

We will discuss all basic formulae used in finding the orthocenter of a triangle. These include:

Slope of the Side:

The slope of all the sides is calculated by using the following formula:

m(slope) = y2 − y1/x2 − x1

Slope of Perpendicular:

By means of the formula below, we can determine the slope of the perpendicular drawn on each side of the triangle.
Perpendicular slope of line = −1/slope of the line
                                               =−1/m

Equation of Altitudes:

We need to determine the equation of the altitudes by using the expression as follows:

(y – y1) = m (x – x1)

After this, we need to solve the algebraic equations to find values corresponding to x and y that are the coordinates of the orthocenter.

Using an orthocenter calculator creates easiness in determining the coordinates of the orthocenter for any triangle.

How to Find the Orthocenter of a Triangle?

We will solve an example to understand the correct use of formulae in finding the orthocenter.
Find the coordinates of the orthocenter of a triangle whose vertices are (2, -3) (8, -2) and (8, 6).

Solution :

The given points are A (2, -3) B (8, -2) and C (8, 6).
Now we need to work for the slope of AC. From that we have to find the slope of the perpendicular line through B.
Slope of AC = (y2 – y1) / (x2 – x1)
A (2, -3) and C (8, 6)
= (6 – (-3)) / (8 – 2)
= 9/6
= 3/2
Slope of the altitude BE = -1/ slope of AC
= -1 / (3/2)
= -2/3
Equation of the altitude BE is given as :
(y – y1) = m (x – x1)
Here B (8, -2) and m = 2/3
y – (-2) = (-2/3) (x – 8)
3(y + 2) = -2 (x – 8)
3y + 6 = -2x + 16
2x + 3y – 16 + 6 = 0
2x + 3y – 10 = 0
Now we need to determine the slope of BC. From that we have to calculate the slope of the perpendicular line through D.
Slope of BC = (y2 – y1) / (x2 – x1)
B (8, -2) and C (8, 6)
= (6 – (-2)) / (8 – 8)
= 8/0 = undefined
Slope of the altitude AD = -1/ slope of AC
= -1/undefined
= 0
Equation of the altitude AD is as follows:
(y – y1) = m (x – x1)
Here A(2, -3) and m = 0
y – (-3) = 0 (x – 2)
y + 3 = 0
y = -3
By putting the value of x in the first equation:
2x + 3(-3) = 10
2x – 9 = 10
2x = 10 + 9
2x = 19
x = 19/2
x = 9.2
So, the orthocenter is (9.2,-3).

You can also verify your results by putting coordinates of all the vertices in orthocenter finder.

How orthocenter calculator works?

Absolute values for coordinates of the orthocenter can be determined by using orthocenter calculator as follows:
Input:

• Insert values of all coordinates against all vertices, respectively.
• Click on ‘calculate’.

 Output:

The calculator calculates:

Exact values of orthocenter coordinates by following each and every step.

FAQ’s:

Is there a different method to find orthocenter for various triangles?

No, the basic method for finding orthocenter is the same regardless the type of the triangle.

Is there any triangle having no Orthocenter?

No, there is not any triangle whose orthocenter does not exist as it is the point of coincidence of the altitudes of the triangle.

What does the orthocenter of a triangle indicates?

The orthocenter of a triangle show the point of concurrency of perpendicular lines.

What is Euler’s Line?

A line passing from all the triangle centers is known as Euler’s line.

Conclusion:

An orthocenter is an important central point of intersection for all triangles. The position of the orthocenter gives the exact idea of the type of the triangle under study. The orthocenter calculator helps you to determine the coordinates of the orthocenter within a span of seconds. Engineers make a vast use of an orthocenter calculator to make their measurements precise and accurate.

References:

From the source of wikipedia: Cheap Flights circles and conics, Orthic triangle, Right triangle, Acute and obtuse triangles, Altitude, Trigonometric functions, equilateral triangle.

From the source of Khan Academy: Common orthocenter and centroid, Proof: Triangle altitudes are concurrent (orthocenter).

From the source of Lumen Learning: The Rectangular Coordinate Systems and Graphs,  Cartesian Coordinate System, Graphing Equations by Plotting Points, Finding x-intercepts and y-intercepts.