Surface Area of a Hemisphere

Surface area:

“The amount of space in three-dimensional shape that covers its outside is termed as surface area”

Formula:

For three-dimensional shapes of surface area is given as:

A = 4 π r^2 square units

Also, you can calculate the radius, volume, surface area and circumference of a sphere shape by using an online sphere calculator to get accurate results.

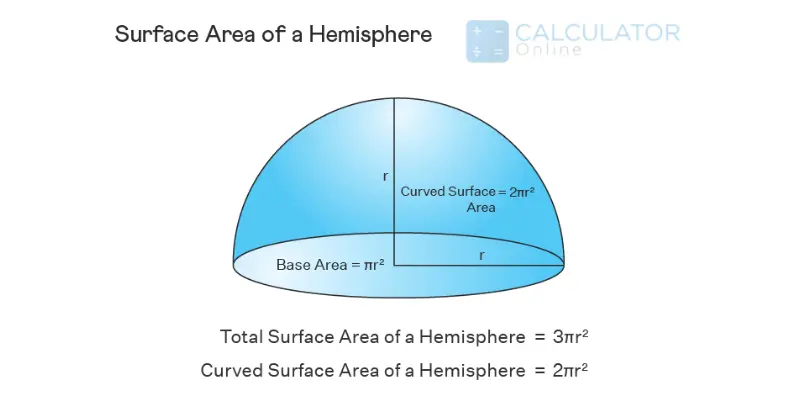
Surface area of hemisphere:

In mathematics, surface area of a hemisphere shape can be defined as:

“Three-dimensional shape where a sphere is cut along a plane that is equidistant from the centre of the sphere”

The hemisphere surface area represents the total region covered by the faces of the hemisphere. The surface area of hemisphere formula is given as:

For CSA of hemisphere = 2πr^2
For TSA of hemisphere = 3πr^2

Hemisphere diagram:

Hemisphere diagram

However, Use an online hemisphere calculator that enables you to perform calculations regarding hemisphere problems accurately.

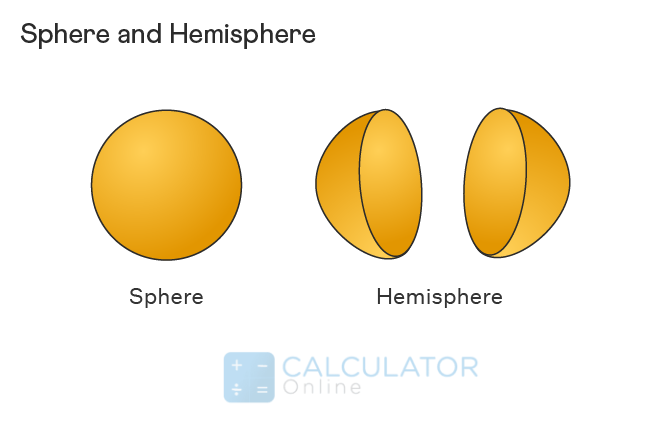
Difference Between Hemisphere and Sphere:

Now we discuss the few differences between a sphere and a hemisphere. These include:

Hemisphere	Sphere
It is a 3D shape that can be obtained by cutting a sphere in half.	This is a 3D round shape specifically used in geometry that has no edges and no vertices.
It has one curved side and one flat side.	This has only a curved side but no flat side.
The volume of a hemisphere = (2/3)πr^3 cubic units	The volume of a sphere = (4/3)πr3 cubic units
Hemisphere has two surface areas, i.e., total surface area = 3πr^2, and curved surface area = 2πr^2.	The surface area of a sphere = 4πr^2

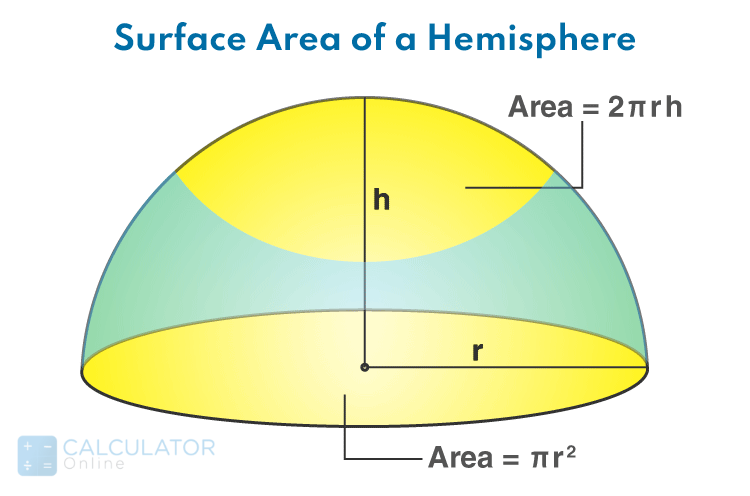
How do find the surface area of a hemisphere?

We can find the lateral surface area of the hemisphere by using the formula of surface area of hemisphere for a hollow or a solid shape. Generally, the surface area of a hemisphere is categorised into two types. These include:

Curved surface area of hemisphere:

The curved surface area is the outer surface of the hemisphere.

We can determine the CSA of a hemisphere from the surface area of a sphere. Since the area of the hemisphere is the half of the sphere. So we can write as:

CSA of hemisphere = (1/2)surface area of the sphere

CSA = (1/2)4πr^2

CSA of hemisphere formula = 2πr^2

Example:

Calculate the curved surface area of a hemisphere whose radius measures 9 units.

(since π = 3.14)

Solution:

The radius (r) of the total curved surface area of the hemisphere = 9 units.

Now let’s substitute the value of r = 9 in the formula of curved surface area of hemisphere.

Curved Surface area of a hemisphere = 2 π r2 = 2 × 3.14 × 9^2 = 2 × 3.14 × 81 = 508.68 units^2

Therefore, CSA of hemisphere = 508.68 units^2

Total surface area of hemisphere:

Now you must think about what is the total surface area of hemisphere. Read below to identify the total surface area of the hemisphere.

“The total surface area of a hemisphere is the curved surface area plus the base area of the hemisphere.”

Total surface area of hemisphere formula is given as:

Total surface area = curved surface area of hemisphere + base area of hemisphere

As we know that the base of the hemisphere is equal to the area of the circle. Therefore,

TSA of hemisphere = 2πr^2 + πr^2 = 3πr^2

TSA of hemisphere formula = 3πr^2 square units

Example:

Find the total surface area of a hemisphere solid whose radius measures 15 units.

(Use π = 3.14)

Solution:

The radius (r) of the total surface area of solid hemisphere = 15 units.

Now let’s substitute the value of r = 15 in the formula of total surface area of hemisphere.

TSA of hemisphere = 3π^2

= 3π × (15)^2

= (3 × 3.14 × 225)

= 2,119.5 units^2

Therefore, total surface area of the hemisphere = 2160.32 units2

Moreover, you can calculate the circumference, radius, diameter, area, sphere surface area, and sphere volume of a circle with the assistance of an online circumference calculator.

Properties of a Hemisphere:

Since the surface area of a hemisphere is the half of a sphere, they have some similar properties including:

A hemisphere area has a curved surface area.
Since hemisphere does not have edges and vertices, like a sphere.
A hemisphere contains one circular base and one curved surface in the surface area.
The diameter of a hemisphere area is a line segment passes through the center of the area and touches its two opposite points on the base of the hemisphere.
The radius of a hemisphere of the surface area is a line segment from the center to a given point on the curved surface of the hemisphere.

The volume of a Hemisphere:

The total capacity of the hemisphere is called its volume. Since it is the number of unit cubes that are covered by the space inside it. Generally, the volume of a hemisphere can be measured in cubic units and written in the form of m3, cm3, in3, etc.

Formula:

Volume of Hemisphere = (2πr^3)/3

Hollow Hemisphere:

If the inside space of a hemisphere is hollow, it is called a hollow hemisphere of the surface area. A hollow hemisphere has two radii that are given as:

An internal radius for the inner circle.
An external radius for the outside circle.