Fibonacci Calculator

Want to find the arbitrary terms of the Fibonacci sequence? The Fibonacci calculator can help. Whether for educational purposes, programming challenges, or financial analysis, this tool generates a list of Fibonacci numbers from start and end values of n. With it, you can also calculate a single number in the Fibonacci Sequence, \( F_n \), It can find the first 250 terms.

What Is The Fibonacci Sequence?

In mathematics, the Fibonacci sequence is a series of numbers in which the first two numbers are 0 and 1 and after that, each term is calculated by the sum of the previous two terms.

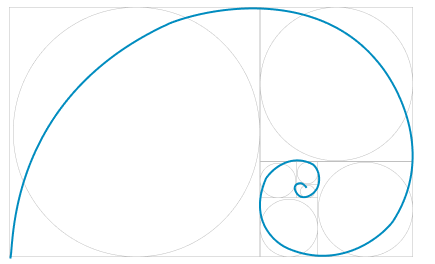
A spiral is commonly used to represent the Fibonacci sequence while making squares with the width of each number.

Fibonacci Image:

What Is The Fibonacci Sequence Formula?

The formula to find the (n+1)th number in the Fibonacci sequence is as follows:

\(\ F_n =\ F_{n-1} + \ F_{n-2}\)Where, n>1

\(\ F_{n-1}\ is\ the\ nth\ Fibonacci\ number\)
\(\ F_{n-2}\ is\ (n-1)th\ Fibonacci\ number\)

To calculate the single Fibonacci number (positive or negative), use the following Fibonacci sequence formula:

\(\ F_{n} = \dfrac{(1+\sqrt{5})^{n}-(1-\sqrt{5})^{n}}{2^{n}\times\sqrt{5}}\)

For only positive integer of n, the simplified formula is:

\(\ F_{n}=\dfrac{(1+\sqrt{5})^{n}}{2^{n}\times \sqrt{5}}\)

Here’s the shorter formula for that:

\(\ F_{n} =\dfrac{\phi^n-\psi^n}{\sqrt5}\)Where

The Greek letter phi represents the Golden Ratio φ = (1 + √5) / 2 ≈ 1.618034…
The Greek letter psi, ψ = (1 – √5) / 2 ≈ -0.618034…

If you are working with positive integers of n, then the shorter Fibonacci Number formula is as below:

\(\ F_{n} =\dfrac{\phi^n}{\sqrt5} =\dfrac{{(1+\sqrt5})^{n}}{2^{n}\times \sqrt{5}}\)

For Negative Fibonacci Numbers:

\(\ F_{-n}=\ (-1)^{n+1}F_{n}\)\(\ Meanwhile,\ when\ -n\ is\ odd,\ F_{-n}= F_n,\ and\ when\ -n\ is\ even,\ F_{-n} =\ -F_n\)

If you are creating a sequence of –n and going towards negative infinity, you can change the above sequence equation to make it a starting point.

\(\ F_0 = 0,\ F_1 = F_2 = 1\ and\)\(\ F_{n}=\ F_{n+2}-F_{n+1}\)

Instead of keeping these formulas remember, use the Fibonacci calculator for convenient computation. It lets you find the precise Fibonacci number and Fibonacci sequence based on specified limits.

How To Calculate Fibonacci?

The Fibonacci Sequence = 0, 1, 1, 2, 3, 5, 8, 13, 21, …. Where 2 is obtained by adding the second and third terms (1+1) and so on. For instance, you can get the next term after 21 by adding 13 and 21.

The Fibonacci sequence rules are:

- The first number in the Fibonacci sequence is,
  \(\ F_0 = 0\)
- The second number in the Fibonacci sequence is,
  \(\ F_1=\ 1\)
  \(\ F_n = F_{(n-1)} + F_{(n-2)},\ where\ n > 1\)

The third number in the Fibonacci sequence can be found as,
\(\ F_2 =\ F_1 +\ F_0 =\ 1 + \ 0 = 1\)
The Fibonacci sequence goes like 0, 1, 1, and so on

Example:

How to calculate the Fibonacci sequence for
\(\ F_n\ for\ n =\ 3\ to\ 7\)

Solution:

\( F_0 = 0 \), \( F_1 = 1 \)

\(\ Fibonacci\ formula:\ F_n = F_{n-1} + F_{n-2} \)

\( F_3 = F_2 + F_1 = 1 + 1 = 2 \)
\( F_4 = F_3 + F_2 = 2 + 1 = 3 \)
\( F_5 = F_4 + F_3 = 3 + 2 = 5 \)
\( F_6 = F_5 + F_4 = 5 + 3 = 8 \)
\( F_7 = F_6 + F_5 = 8 + 5 = 13 \)

So, the Fibonacci sequence for \( F_3 \) to \( F_7 \) is 2, 3, 5, 8, 13.

7th term of the Fibonacci sequence is 13.

The sum of the terms is 31.

Skip manual calculations! Use our Fibonacci sequence calculator for precise computation of Fibonacci numbers and sequences.

FAQ’s:

What Is The Difference Between The Fibonacci Sequence And The Lucas Sequence?

They both are integer sequences but their starting values are different. The key differences are:

Starting Values:

Fibonacci Sequence starts with 0 and 1 while Lucas Sequence starts with 2 and 1.

Initial Terms:

Fibonacci: F(0) = 0, F(1) = 1
Lucas: L(0) = 2, L(1) = 1

General Formulas:

\(\ Fibonacci:\ F_n =\ F_{n-1} + \ F_{n-2},\ where F_{(0)}= 0,\ F_{(1)}=1 \)
\(\ Lucas\ Sequence:\ L_n =\ L_{n-1} + \ L_{n-2}\ where\ L_{(0)}= 0,\ L_{(1)}=1\)

What Are The First 10 Fibonacci Numbers?

The first 10 Fibonacci numbers: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34

for more information, visit the source wikipedia.org.

What Are Two Different Ways To Find The Fibonacci Sequence?

There are two methods to Find The Fibonacci Sequence, which are:

Recursive Relation Method
Golden Ratio Method

What Is The Fibonacci Golden Rule?

The golden rule is the ratio between two numbers approximately equal to 1.618. It is also known as the golden number. Use the golden ratio calculator to obtain the precise value of the golden ratio for your calculations