Golden Ratio Calculator

An online golden ratio calculator is programmed to determine golden ratio value by using either small side, longer side or the sum of two. But wait! Before you move on, let us tell you that you must go through the basic idea of golden ratio.

Let’s dive in!

What Is The Golden Ratio?

In geometrical analysis:

“Two particular numbers are said to be in golden ratio or golden mean or golden proportion if the ratio of their sum to the larger side is equal to their actual ratio”

Golden Ratio Formula:

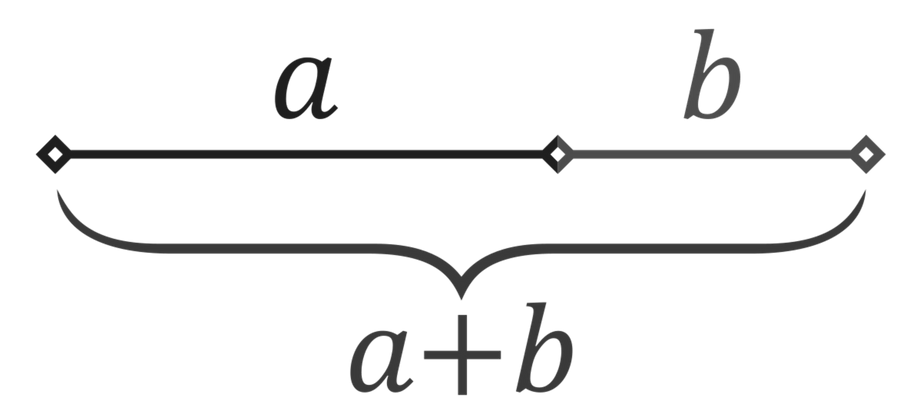
Our free golden ratio calculator is the most efficient way to calculate the math golden ratio. However, when it comes to manual computations, then subjecting to the following equation is a better approach.

$$ ∅ = \frac{A + B}{A} = \frac{A}{B} $$

In actual, the number phi (∅) is calculated as follows:

$$ ∅ = \frac{1 + \sqrt{5}}{2} $$

Which is approximately equal to 1.6180339887498 or simply rounded off to 1.62.

Longer Side Formula:

You can calculate golden ratio by using only the longer side which is determined using the formula given below:

$$ A = B * ∅ $$

Shorter Side Formula:

The following formula helps you in determining the value of short side which is further used to find golden ratio:

$$ B = \frac{A}{∅} $$

Golden Rectangle:

“A particular rectangle having width of A and length of A+B is known as the golden rectangle”

Following are some interesting facts about the golden rectangle:

• If you remove a square from the golden rectangle, the remaining figure is also a golden rectangle
• Now, if you keep on adding a separate square of length A+B, then the resulting figure is also a golden rectangle.

The free golden rectangle calculator also goes with the above criteria and verifies it.

Fibonacci Sequence:

“A particular sequence of the number that is obtained by writing a new number as the sum of the last two preceding numbers is called the Fibonacci Sequence”.

Relationship Among Fibonacci and Golden Ratio:

The most interesting fact here is that the ratio of two successive Fibonacci numbers is nearly equal to that of the golden ratio. Consider the following sequence:

$$ 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, … $$

Now, the following golden ratio chart will display few of the ratios below:

How To Calculate Golden Ratio?

Here we will be solving a couple of golden ratio examples to clarify the idea behind this theory. For better understanding, stay in touch!

Example # 01:

The measure of the shorter side of an image is about 3cm. How to find the golden ratio?

Solution:

As we know that:

$$ A = B * ∅ $$
$$ A = 3 * 1.62 $$
$$ A = 4.86 $$

Carrying out golden ratio measurements with the help of golden ratio equation:

$$ ∅ = \frac{A}{B} $$
$$ ∅ = \frac{4.86}{3} $$
$$ ∅ = 1.62 $$

Example # 02:

Using the golden ratio and the longer side A taken about 6.2cm, determine the shorter side of the ratio.

Solution:

As it is known that:

$$ B = \frac{A}{∅} $$
$$ B = \frac{6.2}{1.62} $$
$$ B = 3.82 $$

To reduce the time of calculations, you can use a free golden ratio calculator which displays results accurately and instantly to save your precious time.

How Golden Ratio Calculator Works?

Make a use of this golden ratio generator that takes a couple of clicks top generate the results. Let us guide you how it works!

Input:

• First of all, select either “longer section”, “shorter section” or “whole”
• After you do so, enter the selected parameter value in the designated field
• Tap the calculate button

Output:

The free golden mean calculator determines:

• Longer section
• Shorter section
• Whole sum
• Golden ratio that is fixed always

FAQ’s:

What is the most special thing about the golden ratio?

The golden ratio number is considered as the most beautiful number in the whole universe. The reason is that this specific number is easily visualized in every image and even the human body itself.

Is the golden ratio determined by the Fibonacci?

Yes, the golden ratio is best calculated using the Fibonacci sequence of the numbers in which every new number is obtained by adding the previous two.

Are golden ratios infinite?

Yes. This is because the golden ratio is determined by the fibonacci sequence best, which is an infinite series of numbers.

What is the angle of the golden ratio?

The angle made by the golden ratio is about \(51.83^\text{o}\) whose cosine is equal to 0.613 or phi.

Who invented the golden ratio?

It is believed that Martin Ohm (1792-1872) was the first person in the whole world who actually used the name golden to describe the golden ratio.

Conclusion:

The golden ratio has broad aspects in the field of art, architecture and designing. Moreover, it plays a key role in estimating the font size used for website writing and maintaining graphic displays. This is why using a free golden ratio calculator can help you out in finding such ratios so that any error could be minimized.

References:

From the source of Wikipedia: Golden mean, Golden ratio, Irrationality, Minimal polynomial, Golden ratio conjugate, Alternative forms, Geometry, Golden triangle

From the source of invisionapp.com: Typography, Cropping and resizing images, Layout, Logo development