Additive Inverse calculator

Use this online additive inverse calculator that helps you to find the additive inverse of a number instantly and accurately. Get going through the article below that is packed with the complete guide about additive reciprocal calculations either manually or by using our free

What’s The Additive Inverse?

In arithmetic analysis, the additive inverse is defined as:

“A particular number that yields zero on addition with the number given”

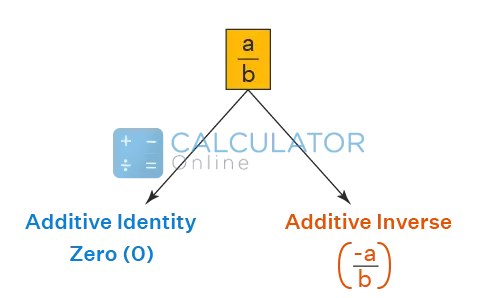
You may cope with any number format just like fraction, decimal, or square root. In such a situation, calculating the opposite or additive inverse seems a little bit difficult. But do not worry as the free additive inverse calculator readily does computations and provides you with the instant outputs. So what are your thoughts on it?

How Do You Find The Additive Inverse of a Number?

If you are up to that which number is the additive reciprocal of the given number, you are in search of the following formula in actual:

Additive Inverse = (-1) * Number

Additive Identity:

In mathematics, zero “0” is referred to as the additive identity. This is because when you add it in any number, fraction, or even decimal, you will get the original number again. Even the additive inverse of the zero is zero.

Additive Inverse Table:

Below here, we have a table representing some of the most used additive inverse numerals of the numbers. Let’s go through these:

For instant verification, you can also make use of this additive inverse calculator to get instant outcomes.

Additive Inverse of Complex Numbers:

For complex numbers, the inverse additive property is almost the same. Let’s discuss it!

Suppose you are given a number as:

Z = a + b𝜾

You can calculate the additive inverse as under:

Additive Inverse = -Z = -(a + b𝜾)

What is the additive inverse of the polynomial?

As you know that the algebraic expressions are the ones that include variables along with real numbers. But the terminology remains the same here too. Let’s take an example!

Suppose you are given a polynomial as:

$$ ax^{2} $$

Now if you wish to calculate the additive inverse of the above polynomial, what you need to do is to add the negative same value to the original value.

Moreover, you can also simplify any algebraic expression by using our rational expression calculator.

Properties of Additive Inverse:

Like every mathematical concept, the additive inverse also exhibits the following characteristics:

• −(−x) = x
• (-x)^2 = x^2
• −(x + y) = (−x) + (−y)
• −(x – y) = y − x
• x − (−y) = x + y
• (−x) × y = x × (−y) = −(x × y)
• (−x) × (−y) = x × y

Numeric Examples:

Right here, we will be resolving a couple of examples to highlight the concept of opposite or additive inverse and let you people understand it better. Stay focused and move on!

Example # 01:

Which number is the additive inverse of 23?

Solution:

Using the additive inverse formula:

Additive Inverse = (-1) * Number

Additive Inverse = (-1) * 23

Additive Inverse = -23

Example # 02:

How to find the additive inverse of 4?

Solution:

Keep following the equation for additive inverse calculations as follows:

Additive Inverse = (-1) * Number

Additive Inverse = (-1) * -4

Additive Inverse = 4

You can also cross check each and every answer calculated by this free additive inverse of a fraction calculator.

How additive inverse calculator works?

Keep going through the guide below that is arranged particularly to use this additive inverse of a fraction calculator.

Input:

• Write down the number in the designated field
• After you are done with it, hit the calculate button

Output:

The free additive property of length calculator calculates:

• Additive inverse of the given number with detailed calculations shown

FAQ’s:

What is the additive inverse of (- 2 )?

2 is the additive inverse of -2 that you could also verify instantly by employing our online additive inverse calculator.

What is the additive inverse of 2 in Z10?

It’s 8 exactly. Do not worry as we are going to explain it. Here the equation to compute the additive inverse is given as:

b = n – a

So we have:

n = 10, a = 2

b = 10 – 2

b = 8

This value can also be justified by this best additive inverse calculator.

What is the sum of 12 ¼ and its additive inverse?

As mentioned earlier , the sum of any number and its additive inverse is always equal to zero. So in this case, it will also be zero. Rest for verification, you may use this additive inverse of a fraction calculator.

What is the additive inverse of negative 9?

The additive reciprocal of 9 is -9.

How is additive inverse used in real life?

We have various real-life applications of additive inverse. For instance, suppose you walk 20 steps in a particular direction, and then move 20 steps back to the initial point. As a whole, you have not taken one step.

What is the difference between additive inverse and absolute value?

The absolute value is actually the distance from zero. And as distance can never be negative, the absolute value of both positive and negative numbers is positive. And additive inverse terminology is already aforementioned. We hope you have already gone through it and understood how to even use the additive property of length calculator.

What is the additive inverse of ab?

It’s -ab. Let’s prove it!

ab + (-ab)

= ab – ab

= 0

What is the additive property of equality?

The additive property of equivalency states that if you add or minus any number on both sides of the equation, the overall effect of the equation remains neutral.

Conclusion:

Additive inverses help you resolve various complex computations in a matter of seconds. That is why in most of the mathematical terminologies, the concept of additive inverse is broadly employed so as to get precise results for any query. And when it comes to the fast and most accurate estimations, this simple to use additive inverse calculator is always there to help you people.

References:

From the source of Wikipedia: Additive inverse, Common examples, Additive identity, Properties

From the source of Khan Academy: Inverse property

From the source of Lumen Learning: Additive and multiplicative inverse of a rational number, reciprocal of a fraction, Identity and Inverse