Math Calculators ▶ Amplitude and Period Calculator
Adblocker Detected
We always struggled to serve you with the best online calculations, thus, there's a humble request to either disable the AD blocker or go with premium plans to use the AD-Free version for calculators.
Disable your Adblocker and refresh your web page 😊
Table of Content
Our free amplitude and period calculator is the best way to find the amplitude, period, and phase shift of the function with respect to trigonometry. You need just once a click, can calculate various amplitude-period parameters. Right now, let’s go to know how to find the period of a trig function of vibrating objects with this period and amplitude calculator.
Let’s move on!
Look at the picture showing where the amplitude, period, phase shift, and vertical shift occur on the graph.
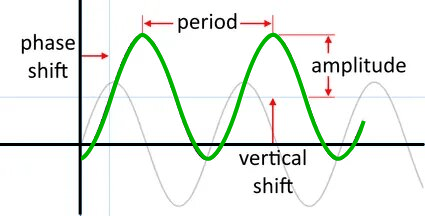
We can write such functions with the given formula
f(x) = A * sin(Bx – C) + D;
or
f(x) = A * cos(Bx – C) + D,
Where;
‘f(x)’ represents function of the sine & cosine
‘B’ represents the period
‘C’ represents the phase shift
‘D’ represents the vertical shift
Right now, you could solve the equations within the above formula and apply the formula to our amplitude period phase shift calculator online
The time required to complete one circle of the vibrating body or wave is known as the period
Formula
y = A sin(Bx + C)
Or
y = A cos(Bx + C) is 2π/|B| radians.
The length of the horizontal axis of the wave is the period after that function begins repeating itself. The value for a simple sine or cosine, is equal to 2π since sin(0) = sin(2π) = sin(4π) = … and the parts in between them are the same. Here, you could find the period and amplitude with the help of a period amplitude calculator.
The maximum displacement covered by a point on a vibrating body or wave from its mean position is called the amplitude of the body.
Formula:
x = A sin (ωt + ϕ)
Or
x = A cos (ωt + ϕ)
The value of amplitude comes from the graph’s centerline. The value of sin or cosine is 1 since the centerline is 0. The function values of sin or cosine range from -1 to 1.
If you find the amplitude period and phase shift of a vibrating body, our amplitude and period calculator is beneficial for you in this regard.
Phase shift is defined as two signals which are at different points of their cycle at a given time.
Or
Inside changes on the wave or vibrating body affect the output (x-) axis value and shift the function left or right is called horizontal shift. You can also determine this particulate shift by subjecting this free and best horizontal shift calculator.
Formula:
F(x) = A sin(Bx − C) + D
Or
F(x) = Acos(Bx − C) + D
The phase shift or horizontal describes how far horizontally the graph moved from regular sine or cosine. If we have two functions unaltered, then its value is equal to 0.
When it comes to find amplitude period and phase shift values, the amplitude and period calculator will help you in this regard.
Outside changes on the wave or vibrating body that affect the output (y-) axis value and shift the function up or down are called vertical shifts.
Formula:
y=Asin(Bx)+D.
Or.
y=Acos(Bx)+D.
The vertical shift describes how far vertically the graph moved from the regular sine or cosine. The value is equal to 0 if we have the two functions unaltered.
Now look at the following examples which are specifically solved to clarify the answer and verify the concept with this amplitude period and phase shift calculator
Example # 1
How to find the period and amplitude of the function f(x) = 3 sin(6(x − 0.5)) + 4 .
Solution
f(x) = 3 sin(6(x − 0.5)) + 4 —————- eq no 1
As the given generic formula is:
f(x) = A * sin(Bx – C) + D —————- eq no 2
When we compared eq no 1 & 2, the following result will be found
amplitude A = 3
period 2π/B = 2π/6 = π/3
phase shift = −0.5 (or 0.5 to the right)
vertical shift D = 4
Example # 2
How to find the period of a trig function of f(x)= 4sin(x)
Solution
f(x)=4sin(x) —————- eq no 1
As the given generic formula is:
f(x) = A * sin(Bx – C) + D —————- eq no 2
When we compared eq no 1 & 2, the following result will be found
Amplitude A= 4
Period B= 1
Phase shift C= 0
Vertical phase D= 0
Let this free amplitude and period calculator resolve the parameters of a trigonometric function. Let’s move on and have a look at its works!
Input
Output
The free find amplitude and period calculator does the following calculations:
The frequency of the waves is inversely proportional to the time period.
Formula:
Frequency = 1/ time period
Or
F = 1/ T
Here you can calculate the period with respect to the amplitude-phase shift period calculator in a span of seconds.
According to the formula of frequency:
F (frequency) = 1 / T (period). f = c / λ = wave speed c (m/s) / wavelength λ (m).
The value by which the graph of the function travels above and below its midline is called the amplitude of the trigonometric function.
There is a difference when sounds are loud, non-linear effect in the electronics and in hearing. If you have time-changing signals then phase shifts can affect the amplitude.
Simply! Phase shift means that the two signals are at different points of their cycle at a given time. Phase shift is calculated as the angle (in degrees or radians) between two points on a circle at the same time.
Although, phase shift could be affected by both shifting right/left and horizontal stretch/shrink. Therefore, the phase shift is positive when the shift is to the right or negative when the shift is to the left.
Yes, the amplitudes of waves are always positive.
An oscilloscope’s timing markers offer the technique to calculate the phase between two signals. The time difference between two corresponding wave points on the signals represents the phase in units of time. Multiplying the ratio of this value to the period of the signals and calculating the phase in degrees.
Use this online graphing trigonometric functions calculator for determining the parameters of amplitude, period, phase shift, and vertical shift. You can perform any type of calculation with respect to trigonometric functions. Although, our amplitude and period calculator find the values within a matter of seconds.
From the source of Wikipedia: Amplitude, Peak amplitude & semi-amplitude, Peak-to-peak amplitude, Pulse amplitude, Amplitude normalization
From the source of khan academy: Midline, amplitude, and period
From the source of lumen learning: Amplitude and wavelength
Everybody needs a calculator at some point, get the ease of calculating anything from the source of calculator-online.net. Feel free to contact us at your convenience!
