Physics Calculators ▶ Wavelength Calculator
Adblocker Detected
We always struggled to serve you with the best online calculations, thus, there's a humble request to either disable the AD blocker or go with premium plans to use the AD-Free version for calculators.
Disable your Adblocker and refresh your web page 😊
Table of Content
An online wavelength calculator is designed to evaluate the wavelength, wave velocity and frequency of a wave. You can calculate any disturbance in a wave passing through a certain medium by using a wave calculator.
Let us discuss the phenomenon of wavelength in detail.
“A wave is considered as a disturbance in any medium that transfer energy from one point to another”
The wavelength is defined as the distance over which the entire shape of the wave repeats. This repetition happens after a fixed interval of time.
The SI unit of the wavelength is meter or ‘m’.
By subjecting to the following equation, you can find wavelength to frequency relationship easily.
λ = v/f
Where;
λ = wavelength,
v = velocity of the wave,
f = frequency of the wave.
Our free online wavelength calculator uses the same relation to calculate absolute results.
The number of the wave per unit length is termed as wave number. It is always reciprocal to that of the wavelength. Every wave has its own specific wave number.
According to System International, the unit of wave number is per meter or 1 / m.
The rate of change of speed in a specific direction is known as velocity. The term preset velocity means a fixed velocity in certain media under particular conditions of temperature and pressure. In the vast galaxy of Science, the preset velocities of sound and light in different media are as follows:
| Wave Media | Preset Velocity |
| Light in Vacuum | 299792458 |
| Light in Air | 299702547 |
| Light in Water | 225238511 |
| Light in Glass | 199861639 |
| Sound in Air at 20 °C | 343 |
| Sound in Air at 40 °C | 355 |
| Sound in Rubber | 60 |
| Sound in Lead | 1210 |
| Sound in Gold | 3240 |
| Sound in Glass | 4540 |
| Sound in Copper | 4600 |
| Sound in Aluminum | 6320 |
Following are the most important quantities on which the structure of the wave depends:
Wave velocity:
The speed at which the wave propagates in a medium is called wave velocity. It is measured in meter per second (m/s or m s⁻¹).
There exists a direct relationship between the wavelength and velocity. If the velocity of a wave is increased, its wavelength also increases. Similarly, decreasing the velocity will result in decreasing wavelength of the medium.
V = λ * f
Our wave speed calculator also accounts for the same formula to calculate the wave speed precisely.
Wave frequency:
The number of cycles completed by a wave during a certain time is known as the wave frequency. The frequency of a wave is always measured in the units of waves per seconds or cycles per seconds or simply Hertz(Hz). The frequency is reciprocal to the time period such as:
f= 1/t
By making considerable adjustments in wavelength equation, we can find the frequency of the wave as follows:
f= v / λ
Time period:
It refers to the amount of time in which a cycle of the wave is completed. It is inversely proportional to the frequency as:
t = 1/f
In order to determine the frequency to wavelength relationship, let us solve a few examples below:
Example # 01:
Determine the wavelength of the light in space bearing a frequency of 3 Hz.
Solution:
Speed of light in vacuum is given as:
c = 300000000 m / s
Using wavelength frequency equation, we have:
λ = v/f
λ = 300000000 / 3
λ = 100000000 m
In order to determine the wave number, you must assign to our free online wavelength to frequency calculator.
Example #02:
How to find wavelength from frequency of a light given as 4.3 Hz and velocity as 2 m / s. Also calculate the wave number.
Solution:
We know that:
λ = v/f
Putting the values in wavelength formula:
λ = 2 / 4.3
λ = 0.4651 m
Wave number = 1 / wavelength
n = 1 / λ
n = 1 / 0.4651
n = 2.1500 1 / m
Example # 03:
The wavelength of a light passing through a medium is 1.00 m and the frequency is 2 Hz. Evaluate the wave velocity.
Solution:
Using the wavelength formula, we have;
λ = v/f
Or;
v = λ * f
v = 1 * 2
v = 2 m / s
Example # 04:
How to find frequency from wavelength of sound wave to be 3.0 m travelling through gold?
Solution:
By making amendments in the wavelength equation;
λ = v/f
Or;
f = v / λ
= 3240 / 3
= 1080Hz
Whenever you want to find the wavelength, you can use free frequency to wavelength calculator to generate accurate results. Let us see what you have to do.
Input:
So, what you need to find, choose one from the given drop-down list:
After selecting;
Output:
Corresponding to the input selected, the calculator calculates either:
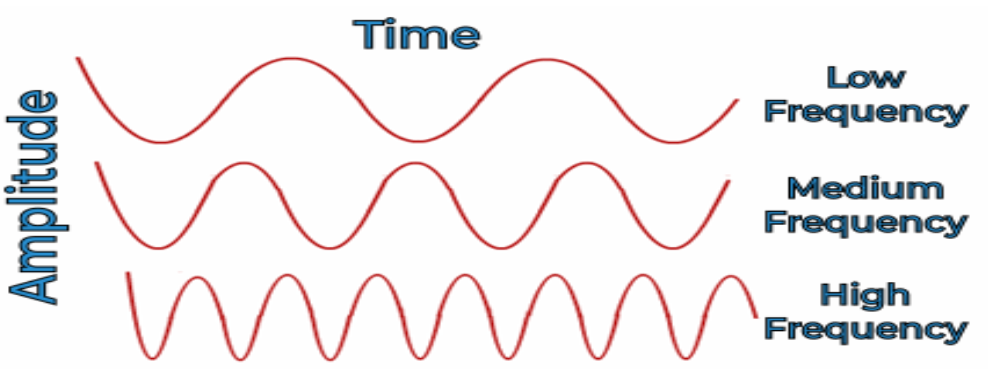
Amplitude is the maximum distance covered by a wave from its equilibrium position.
A wave in which the vibration of the medium is in the direction of the wave is called longitudinal wave.
The direction of a transverse wave is always perpendicular to that of the medium in which it propagates.
Crests are the highest point of a transverse waves whereas the troughs are the lowest points.
For a longitudinal wave, the rarefactions and compressions are equal to crests and troughs for transverse waves.
The wavelength is actually the distance between two consecutive crests and troughs. By measuring the wavelength of a wave, you can measure the energy of the wave. Every wave has its own wavelength and you can easily determine the frequency and velocity by using our free online wavelength calculator.
From the source of wikipedia: Sinusoidal waves, Standing waves, General media, Wave packets, Interference and diffraction, Single-slit diffraction, Diffraction-limited resolution, Subwavelength, Angular wavelength
From the source of lumen learning: AMPLITUDE AND WAVELENGTH, LIGHT WAVES, SOUND WAVES.
From the source of khan academy: Standing waves on strings, Wavelength and frequency for a standing wave, Harmonics.
Everybody needs a calculator at some point, get the ease of calculating anything from the source of calculator-online.net. Feel free to contact us at your convenience!
