Instantaneous Rate of Change Calculator

An online instantaneous rate of change calculator helps you to find instantaneous rate of change at a point. Try to this iroc calculator to understand that demonstrate the rate of change at a given particular value of ‘\(x\)’. Give a read to the given context to understand how to calculate instantaneous rate of change and its formula. But, let’s start with some fundamentals!

What is Instantaneous Rate of Change?

In Mathematics, it is defined as the change in the rate at a specific point. It is similar to the rate of change in the derivative value of a function at any particular instant. If we draw a graph for instantaneous rate of change at a specific point, then the obtained graph will be the same as the tangent line slope. Well, for convenience, you ought to use slope calculator that let’s you to find the slope between two different points in the Cartesian coordinate plane.

Instantaneous Rate of Change on a Graph:

If there is a graph that has your position vs. time and it is not a straight line, then to find instantaneous rate of change you can draw a tangent line, which only hits the graph at one point. The slope of this tangent will provide you the instantaneous rate of change accurately on that specific point.

Instantaneous Rate of Change Formula:

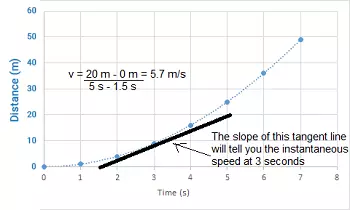
It is easy and simple to calculate the instantaneous rate of change of any function. Let’s suppose f is a function of x, then the instantaneous rate of change at the \(x=a\) will be the average rate of change over a short time period. In terms of the formula:

•  \( \lim_{x\to a}Δf / Δx=\lim_{x\to a}f(x)−f(a) / x−ac\).

This is the slope of the line tangent to \( y=f(x) \) at the point \( (a,f(a))\). It can be demonstrated as a limit as follows:

• \(\lim_{h\to 0}f(a+h)−f(a) / h\)
• in the above equation h is replaced for \( x−a \).
• If this limit exists, we call it the derivative of f at \(x=a\).

This is the slope of the line tangent to \( y=f(x) \) at the point \( (a,f(a)) \). It can also be written as a limit

• \(\lim_{h\to 0}f(a+h) −f(a)h\)
• where \(h\) is substituted for \(x−a\).
• when limit exists, it will be recognized as the derivative of: \(f at x=a\).

Apart from such complex formula, an online instantaneous rate of change calculator is the best way to do instant calculations. Just fill in the fields and go with the flow. Also, the online limit calculator is the best way to solve different limit directions for a given at any point. So, if it comes to derivative calculations, then use an online derivative calculator to differentiate the given values and get a step-by-step result.

How to find Instantaneous Rate of Change?

You can calculate instantaneous rate of change at a point as follows:

Input:

• First of all, just Enter the function or equation in the respective input filed.
• Now enter the value of\( x\). you can select negative or positive as per your need.
• Click the calculate button.

Output:

• This instantaneous rate of change calculator will display the review of your input.
• Secondly you will have the rate of change at a specific point.

FAQs:

Can you measure Instantaneous Speed Directly?

It can never be measured as there is no way in the real world to do anything instantaneously. It will take some time to perform. However, you can find instantaneous rate of change at any particular moment as soon as the speed and position change.

What is a Negative instantaneous Rate of Change?

Whenever the instantaneous rate of change is negative, it illustrates that the function is decreasing at that point. As an example to calculate instantaneous rate, if the given function is = mx+b when m is positive, it represents the increase in function but if it will be negative it means a decrease in function.

What is another name for Instantaneous Rate of Change?

It is also recognized as a differential coefficient, fluxion.

Is Average Rate of Change the same as Instantaneous Rate of Change?

The main difference between these two terms is that the average rate of change will be over a range, whereas the instantaneous rate of change is applied at any specific point and can be directly measured by instantaneous rate calculator.

Ending Note:

Instantaneous Rate of Change Calculator is specifically designed for learning and educational purposes. It displays the rate of change for the given inputs within seconds therefore it will be a great help in making quick calculations. To avoid the risk of error in complex calculation while calculating instantaneous rate of change at a point it is one of the best ways to approach. Give it a try and learn quickly!

References:

From the source of Wikipedia: Rate of change (explore authorized information)

Get the organized information from brightstorm: Concept about Instantaneous Rate of Change – Concept

From the source of toppr: Compute rate of change (solved questions and examples)