Adblocker Detected

We always struggled to serve you with the best online calculations, thus, there's a humble request to either disable the AD blocker or go with premium plans to use the AD-Free version for calculators.
Disable your Adblocker and refresh your web page 😊
The e calculator helps you to calculate the value of e to the power of x. They are known as exponential functions such as \(e^x, 10^x, and a^x\). X can be any number or a power value of your choice and e is the exponent. This calculator also displays a simple solution to enhance your understanding. Keep on reading to know what does e equal to and how to calculate e. However, take a start from some basics.
E to the x is one of the most significant constants in the field of mathematics. We cannot write the value of e as a fraction and it has an immeasurable number of decimal places. In arithmetic, it is known as Euler’s number or the natural number.
The value of e to the x is equal to \(2. 71828182845904536565652… and continue!\)
Because of such an infinite value, the technique of round-off and approximation becomes essential. Furthermore, e is the base of the natural logarithm and we use it in the natural exponential function:
E is the limit of \( (1 + \frac{1}{n})^n\) as “n” approaches infinity, and we can calculate it as the sum of the infinite series.
You can use this free online log calculator that help to calculate logs and inverse log of any number base.
On a calculator display, e represents the exponent of 10 and followed by another number. That number will be known as the value of the exponent. For example, an e on calculator can display the number 25 trillion as:
In this example \(13\) is the exponent of \(10\) and \(2.5\) is the value of the exponent.
For convenience, an exponent calculator online lets you solve the exponent operations as well as find the value of any positive or negative integer raised to the nth power.
There are numerous ways to calculate e to the x but there is not even a single technique on which we can completely depend for the accuracy of our answer. The reason is that e is irrational and its digits go on repeating without any limit. Though, we can determine it as follows:
Euler also used this technique to calculate e to 18 decimal places. However, you can try e calculator to avoid this hustle!
It might be difficult to graph it because all of its y-values will be decimal approximations. Consequently, you have to round off those values to plot a graph easily. Graph of e of x is as follows:
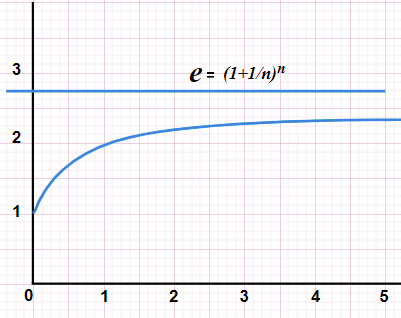
| n | (1 + 1/n) |
| 1 | 2.00000 |
| 2 | 2.25000 |
| 5 | 2.48832 |
| 10 | 2.59374 |
| 100 | 2.70481 |
| 1,000 | 2.71692 |
| 10,000 | 2.71815 |
| 100,000 | 2.71827 |
while plotting the graph of \( e^x \) function, always remember that the slope of the tangent line to any point will be equal to its y-coordinate at that point.
For a quick reference of values, you can Mention the following \(e^x\) table. All values can be generated by using an e calculator.
| e^x | Euler’s number |
| e1 | 2.71828 |
| e2 | 7.38906 |
| e3 | 20.08554 |
| e4 | 54.59815 |
| e5 | 148.41316 |
| e6 | 403.42879 |
| e7 | 1096.63316 |
E on calculator can b figured out just in two steps as follow:
The calculator will calculate:
A calculator allowed you to make unlimited calculations without any cost.
E infinity value will be equal to Zero. The reason is that when we multiply a constant number by infinity times the answer will be zero. E infinity value means that we have to raise the e at a very high rate thus it will result in a very high number. So as a conclusion we can say that e raised to the infinity of power is infinity. However, the case will be different if we have a definite number. For example, e to the power of 1 will be equal to \( 2.718282……\) etc.
A mathematician named “Leonhard Euler” has discovered the e number and calculated its value to 23 decimal places. The certain properties of e number made it a “natural” number as a logarithmic base.
It is considered as a function of Real numbers and has an infinite domain and range equal to 0, ∞. Thus it takes only positive values and 0 is the only value that ex cannot take.
These two numbers are not associated. π was discovered at the beginning of geometry, whereas e is a relatively new concept that is related to the theory of limits and functional analysis.
People can be able to determine the value of e raised to the power of x in a fraction of seconds with the assistance of this free e calculator. As you can see the value of E involves infinity, consequently its manual calculations might be tricky, quite troublesome, and time-taking. So feel free to use this tool for educational and learning purposes as you support saving your time and efforts.
From the source of Wikipedia: Standard normal distribution, Derangements, Optimal planning problems.
From the source of Popular Mechanics: Euler’s Constant, Who Discovered Euler’s Constant?
Use Euler’s Constant to Calculate Compounding Interest.
From the source of Aops Online: Euler’s number, Euler’s Number as the Base of Logarithms and Exponential Functions, Euler’s Number and Calculus, Euler’s Number and Calculus.