Exponent Calculator

The exponent calculator determines that how many times a number (the base) is multiplied by itself. It has simple interface, just put the base and its exponents to calculate the exponent operation of large base integers and real numbers, including expressions that use the irrational number e as a bases.

What is an Exponent?

In Mathematics, exponent mean the power. It indicates how many copies of a number multiply together. It's written as a small raised number to the right of the base.

For Example:

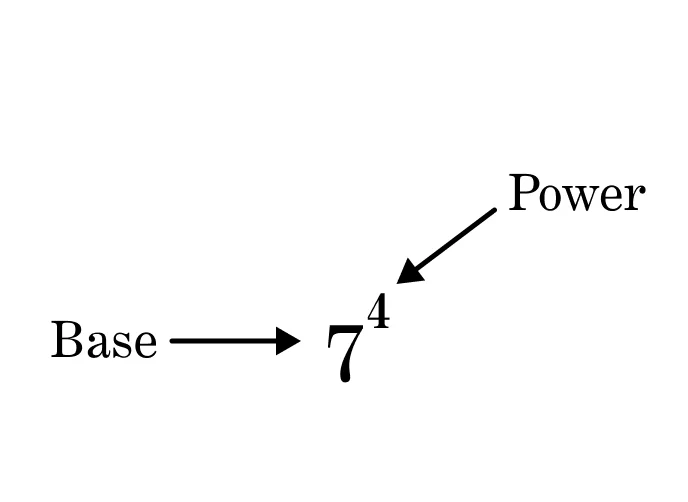
Exponent calculator example

In this example, 4 copies of 7 are multiplied together to give 2401 as 7*7*7*7.

Basic Exponent Rules:

Product Rule:

When multiplying a positive base by two different exponents, then the resultant is the exponents of bases. \(a^m.a^n = a^{m+n}\)

Quotient Rule:

When dividing a positive or negative bases by two different exponents, then the difference of both the exponents is the power of bases. \( {\frac{a^m}{a^n}} = a^{m-n}\)

Zero Rule:

The exponents of any number will be equal to 1. \( b^0 = 1 \) Where b is a base (positive or negative)

Power of Exponent Rule:

When a given bases having the power of its exponents, then both are multiplied together to get the single power. \(({a^m})^{n} = {a}^{mn}\)

Power of the Product of Two Numbers:

When the product of two integers having the power, then both the integers have the same power but separately. \((ab)^x = a^x*b^x\)

Negative Power Property:

When the power of the some integer is the negative number, then it will be equal to the reciprocal of the number. While the rules for fractional exponents with negative bases are the same. \(a^-x = {\frac{1}{a^x}}\)

Example

Find 3 raised to 7? where, 3 is a base and 7 is a exponent.

Solution:

The formula for non-negative is:

\((x)^n = x*x*x*x*……..n\)

Here, x is 3 & n is 7.

So,

\((3)^7= 3*3*3*3*3*3*3\)

\((3)^7= 2187\)

Table to Determine the nth Power of a Number:

A fractional exponent, like a²/³ is where the exponent is a fraction. It can be written as a root as well, like ³√a. Now, calculating exponents for both negative as well as positive integers become very easy with the exponent calculator. Look at the table below for some common values of integers:

0.1^3	0.001
0.1^4	0.0001
0.2^3	0.008
0.5^3	0.125
0.5^4	0.0625
0.5^3	0.125
1.2^4	2.0736
1.02^10	1.21899
1.03^10	1.34392
1.2^5	2.48832
1.3^5	3.71293
1.3^3	2.197
1.4^10	28.92547
1.05^5	1.27628
1.05^3	1.157625
1.05^10	1.62889
1.06^10	1.79085
2^3	8
2^4	16
2^5	32
2^6	64
2^7	128
2^9	512
2^10	1024
2^15	32768
2^28	268435456
3^2	9
3^3	27
3^4	81
3^5	243
3^8	6561
3^9	19683
3^12	531441
3 to what power equals 81	3⁴
4^3	64
4^4	256
4.3^5	1470.08443
4^7	16384
7^3	343
12^2	144
2.5^3	15.625
2.19^5	50.3756397099
12^3	1728
10 exponents 3	1000
24^2	576

References:

Wikipedia: Definition & rules of exponentiation Sciencing.com: How to find it manually.

Other languages: Kalkulator Potęg, Kalkulator Eksponen, Üslü Sayı Hesaplama, Potenzrechnung, 指数計算, 지수 계산기, Mocniny Kalkulačka, Calculadora De Potencia, Calcul Puissance, Calculadora De Potencias, Calcolo Potenza, Калькулятор Экспоненты, Potenssi Laskin, Potens Kalkulator.

EN	PL	ID
TR	DE	JA
KO	CS	PT
FR	ES	IT
RU	FI	NO

EN	PL	ID
TR	DE	JA
KO	CS	PT
FR	ES	IT
RU	FI	NO