Normal Force Calculator

Try this normal force calculator to determine the amount of force a surface applies on an object to prevent it from falling. 

What Is Normal Force?

The normal force is exerted on an object by a surface. For instance, you have a glass and you put it on a table, and the gravitational force pulls the glass downward. To stop the glass from going down the table exerts a force on it. 

This force that is exerted by the table is known as the normal force.

It is denoted by \(F_N\) or N and the unit that is used for the normal force is Newton. This normal force follows the principle of Newton’s Third Law of Motion.

How To Calculate Normal Force On Incline & Flat Surfaces?

Normal force acts perpendicular to the surface and it changes on whether the object is on an incline or a flat surface.

Normal Force Formula:

The formula that is used for knowing the normal force on a thing that is placed on a horizontal surface is as follows:

\(Normal\ Force\ =\ F_N = m.g\)

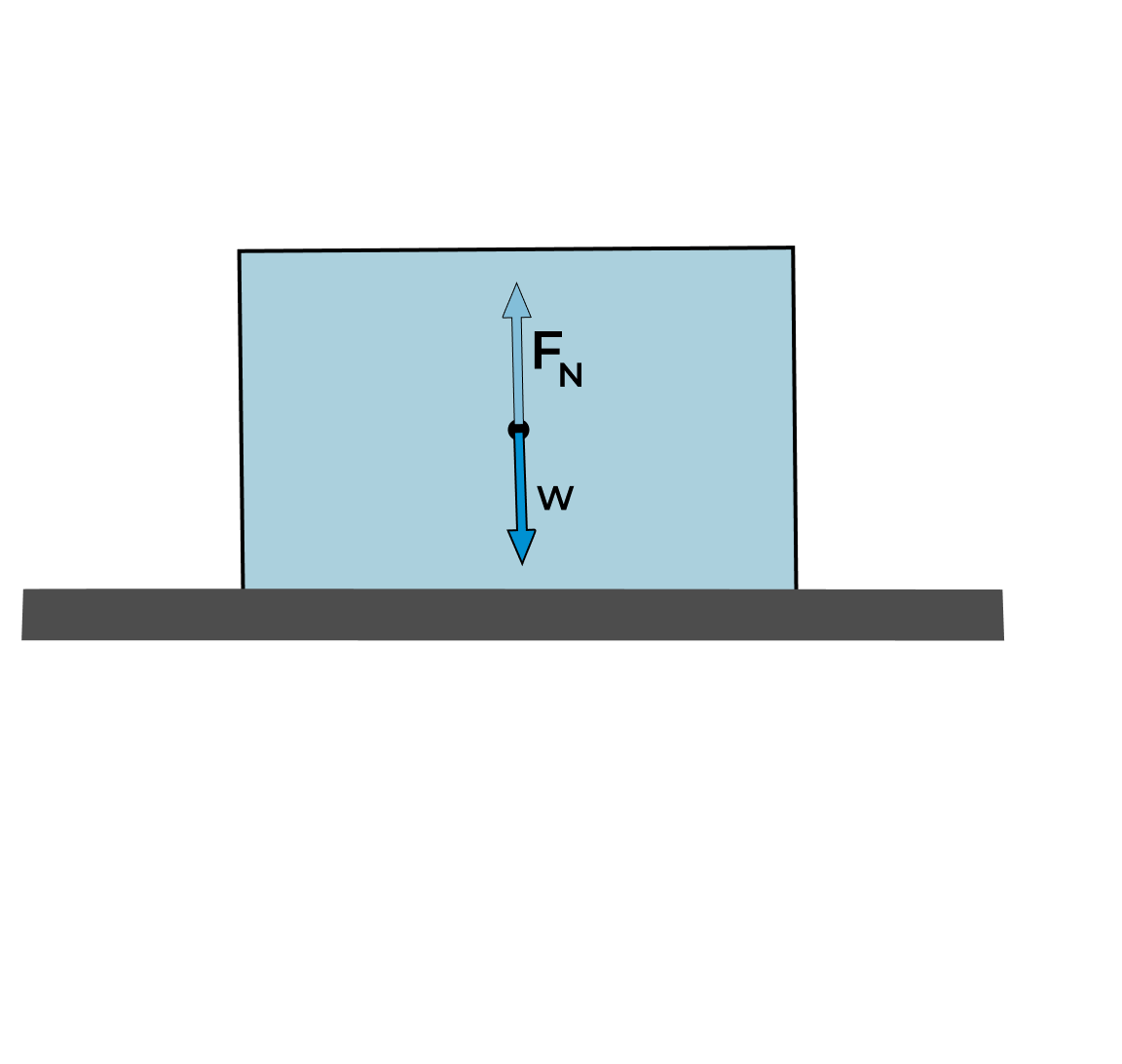
Where

• m is representative of the mass of an object
• g is the gravitational acceleration

If the object is placed on an inclined surface then the normal force on an incline is:

\(Normal\ Force\ =\ F_N = m.g.cos(a)\)

Where 

• a is the surface inclination angle

When the object is placed on a horizontal surface and an external force acts on it in an upward direction then the normal force equation is as follows:

\(Normal\ Force\ =\ F_N = m.g – F.sin(x)\)

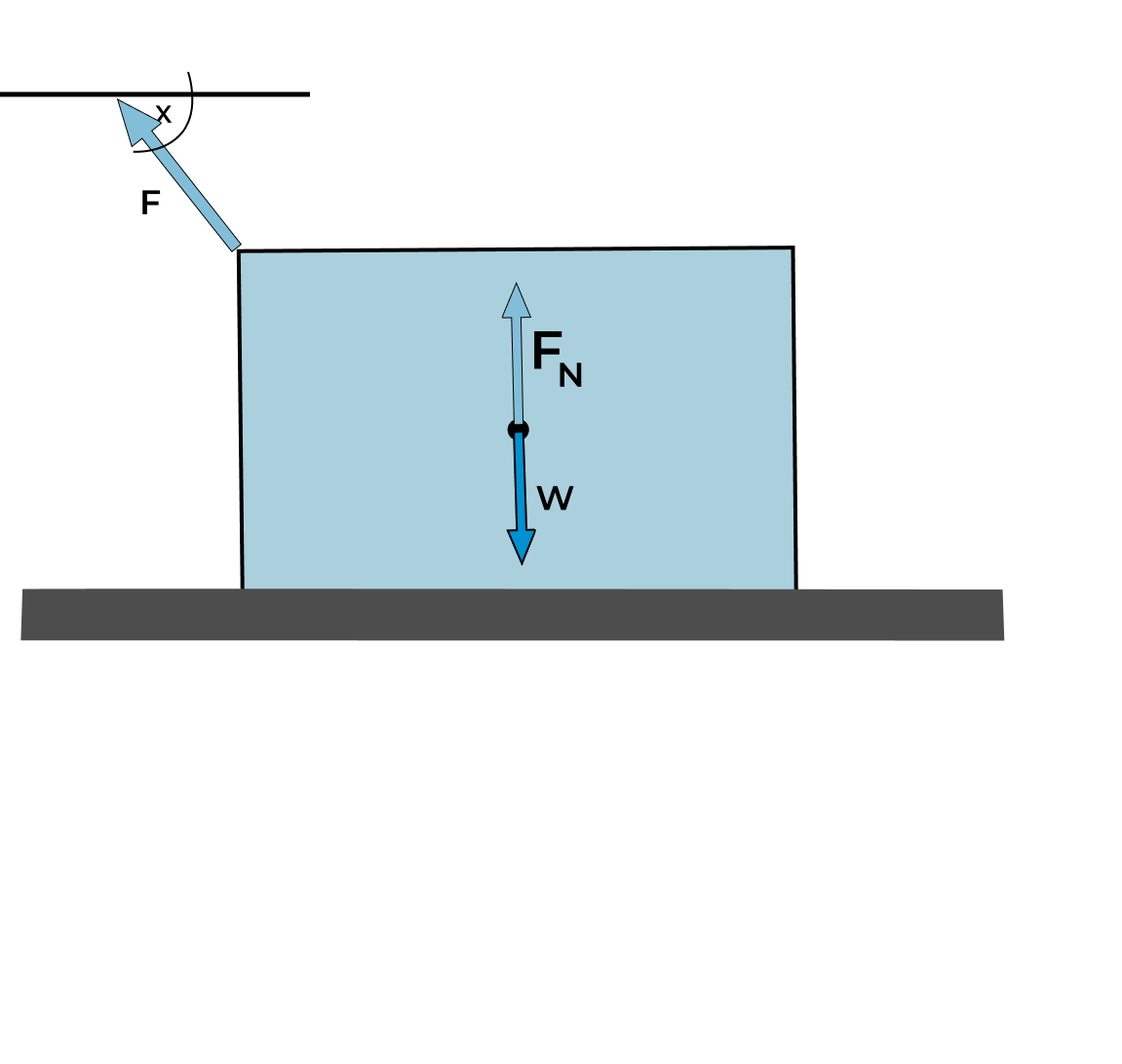
Where

• F is the external force that acts on the object
• x is the angle between the outward force and the surface

If the object is present on a horizontal surface and an external force acts on it in the downward direction then the formula of normal force is:

\(Normal\ Force\ =\ F_N = m.g + F.sin(x)\)

Normal Force Examples:

1. Let’s suppose an object is placed on a table if the mass of the object is 1 kg. The Angle of inclination is 45°, so how to find normal force?

Solution:

Mass = m = 1 Kg

Angle = θ = 45°

\(F_N  = m * g * cos(α)\)

Substituting the values in the normal force formula

\(\text{Normal Force} = F_{N}\)

= 1 * 9.8 * cos (45°)

= 6.92N

2. Suppose An object of mass of 10 kg is sliding down with a force of 200 N from a slant surface at an angle of 30°. Calculate the normal force being exerted on it.

Solution:

Given that:

F = 200 N

m = 20 kg

g = 9.8 ms^-2

θ = 30°

Using the formula we get,

\(Normal\ Force\ =\ F_N  = mg + Fsin θ\)

\(Normal\ Force\ =\ F_N  = 20 (9.8) + 200* sin (30°)\)

\(F_N  = 196 + 200 (1/2)\)

\(F_N  = 196 + 100\)

\(F_N  = 296 N\)