Orbital Period Calculator

Use this calculator to estimate the orbital period of a binary system or a satellite around the Earth.

The orbital period calculator simply takes the central body density, as well as the semi-major axis, first body, and second body mass information to predict the orbital period. 

Orbital Period Definition:

“The time that an object or satellite takes in completion of one complete rotation around another big object is known as the orbital period”

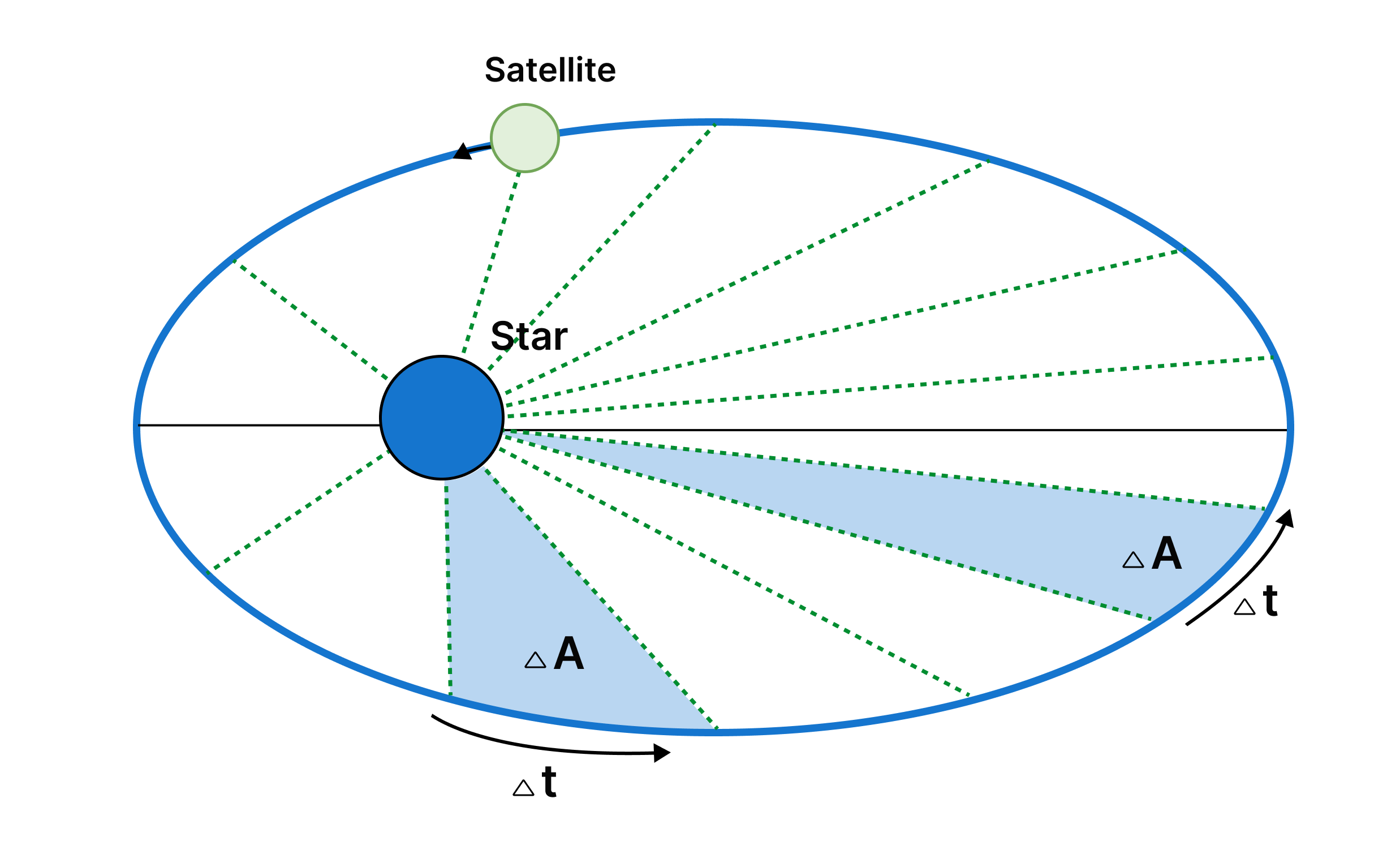
This concept is used for celestial bodies, such as planets orbiting stars or moons. It’s an important parameter governed by the principles outlined in Kepler’s laws of planetary motion.

Types of Orbits:

Two types of the orbits are:

Low Earth Orbit:

This is the orbit that is present very close to the surface of the earth. You can calculate it only with the mean density of the central mass. 

Binary Star System:

In this system, two stars having similar masses are close to each other. They rotate around each other without a material central body.

Orbital Period Equation:

The formula that is used for the low earth orbit is as follows:

\(T = \sqrt(\dfrac{3\pi}{G*P})\)

To calculate the orbital period of a binary star system, use the following formula:

\(T_b=2\pi \sqrt(\dfrac{a^{3}}{G(M_1 + M_2})\)

How To Calculate Orbital Period?

Go through the following steps to calculate the orbital period:

For Low Earth Orbit:

• Note down the information that you have on paper
• Multiply 3 by the value of pi
• Now multiply the Universal gravitational constant by the mean density of the central body
• Put the values in the above-mentioned orbital period formula as we have done in the following example. 

1) Example:

Suppose the central body density is 6.51 g/cm^3, how to find orbital period for low earth orbit?

Solution:

Given that:

Density = P = 6.51 g/cm^3 

Convert it into k/m^3

5.51 * 1000 * (1 /100)^3 = 6510

P = 6510 kg/m^3

As we know G is the gravitational constant 

\(G =\ 6.67 * 10^{-11}\ m^{3}\ kg^{-1}\ s^{-2}/)

Put these values in the orbital period equation

\(T = \sqrt(\dfrac{3\pi}{G*P})\)

\(T = \sqrt(\dfrac{3*3.1459}{(6.67*10^{-11})* 6510})\

Here we have divided the answer with 3600 to convert it into hours

\(T = \dfrac{4662.079}{3600}\)

T = 1.2950 hours 

For Binary Star System:

• Gather the information about the relevant parameters such as the semi-major axis, first body mass, and second body mass
• Write down the orbital period formula
• Put the values in the formula for calculating orbital period as we have done below

2) Example:

Suppose you have the following terms:

• Semi-major axis =  5 m
• Mass of first body = 30 kg
• Second Body Mass = 20 kg

Find the Orbital Period.

Solution:

Given that:

A = 5 m 

\(M_1 = 30 kg\)

\(M_2 = 20 kg\)

Now put these values in the orbital period formula:

\(T_b=2\pi \sqrt(\dfrac{a^{3}}{G(M_1 + M_2})\)

\(T_b=2\pi \sqrt(\dfrac{(5)^{3}}{(6.67*10^{-11})(30 + 20)})\)

Here we have divided the answer with 3600 to change it into hours

\(T = \dfrac{1218097.344}{3600}\)

T = 338. 3 hours

References:

Wikipedia.org: Orbital Period.