Center of Mass Calculator

An online center of mass calculator is intuitively designed to find center of mass of single or multiple objects in one, two or three dimensions, respectively. Here, you should have a proper understanding of some quantitative terms that are described below.

Keep scrolling down!

What Is Center Of Mass (COM)?

“A point where the whole mass of an object becomes concentrated is termed center of mass

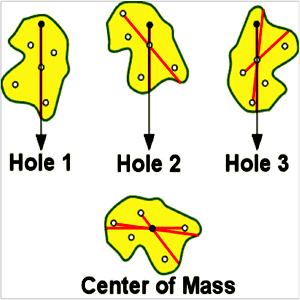
Brief explanation:

Whenever we are interested in studying the dynamics regarding the system motion of particles as a whole, then we do not need to know about the dynamics of each and every particle separately. What we need to focus on is the pivot point that is the center of mass.
Basically it is a point where an object can be balanced perfectly if suspended horizontally.

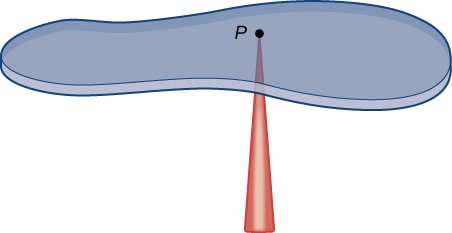
As there exist some external forces exerted by surrounding bodies also, it must be kept in mind that the resultant of all these forces is directed to the center of mass.

Center Of Gravity(COG):

“It is a point where the gravitational force acts to pull it towards the ground.”

The center of gravity changes with respect to the position of an object or human body and is not always fixed. In a uniform gravitational field, the center of gravity calculation is same as it is for the center of mass.

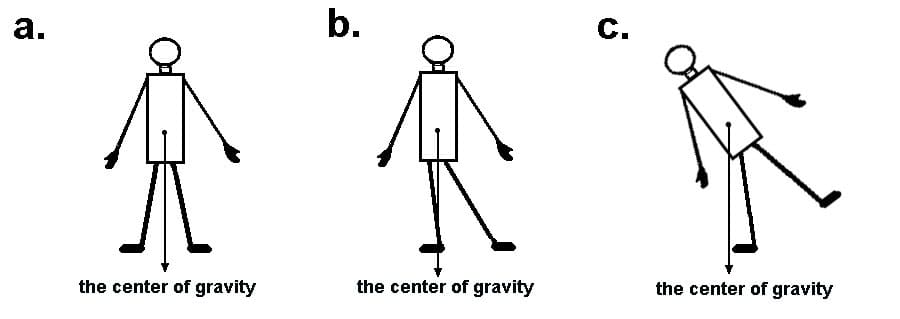
Relationship Between Center Of Mass And Center Of Gravity:

In a uniform gravitational field, both the center of mass and center of gravity are considered equal. But in case there is a non-uniform gravitational field, these terms get different from each other. The reason is that the center of mass is a fixed point but the center of gravity is not.

Center Of Mass Equation:

You can easily calculate center of mass with the help of the formula given below:

$$ center of mass = \frac{\left(m_{1}r_{1} + m_{2}r_{2} + … + m_{n}r_{n}\right)}{\left(m_{1} + m_{2} + … + m_{n}\right)} $$

Where:

m = mass of the individual objects
n = number of the objects
r = distance of point from reference position

The above is a general form of center of mass equation. However, you can also perform a center of mass calculation in either one, two or three dimensional coordinate system, respectively.

COM For Two Dimensional System:

In case we have a 2D system, the center of mass calculations can be performed as follows:

$$ x_{com} = \frac{1}{M} * Sum m_{n}x_{n} $$

$$ y_{com} = \frac{1}{M} * Sum m_{n}y_{n} $$

Where:

n = 1, 2, 3, …

COM For Three Dimensional System:

You can calculate center of mass in a 3D system by following the equations below:

$$ x_{com} = \frac{1}{M} * Sum m_{n}x_{n} $$

$$ y_{com} = \frac{1}{M} * Sum m_{n}y_{n} $$

$$ z_{com} = \frac{1}{M} * Sum m_{n}z_{n} $$

Where:

n = 1, 2, 3, …

Our free online center of mass calculator depicts the center of mass by using the same formulae.

How To Calculate Center Of Mass?

You can find center of mass easily using a center mass equation. Let us solve a couple of examples to clarify the concept in more depth.

Example # 01:

The mass of an object is 10kg and its reference distance is about 3.5m. Similarly we have a second object having a mass of 3kg and reference distance as 2m. How to calculate center of mass?

Solution:

Using the general center of mass equation:

$$ center of mass = \frac{\left(m_{1}r_{1} + m_{2}r_{2} + … + m_{n}r_{n}\right)}{\left(m_{1} + m_{2} + … + m_{n}\right)} $$

Putting the values of both masses and their distances from the zero point as follows:

$$ center of mass = \frac{(10)(3.5) + (3)(2)}{10 + 3} $$

$$ center of mass = \frac{(10)(3.5) + (3)(2)}{10 + 3} $$

$$ center of mass = \frac{41}{13} $$

$$ center of mass = 3.153m $$

Here, our free online center of mass calculator calculates the same results but instantly to save your precious time.

Example # 02:

How to find the center of mass of two objects having following values below:

Mass of one object = 2kg
X coordinate of first object = 1.5cm
Y coordinate of first object = 2cm

Mass of second object = 1kg
X coordinate of second object = 3cm
Y coordinate of second object = 4cm

Solution:

We know that for a 2D system:

$$ x_{com} = \frac{1}{M} * Sum m_{n}x_{n} $$

$$ y_{com} = \frac{1}{M} * Sum m_{n}y_{n} $$

Performing center of mass calculation:

$$ x_{com} = \frac{1}{M} * Sum m_{n}x_{n} $$

$$ x_{com} = \frac{1}{2 + 1} * (2)(1.5) + (1)(3) $$

$$ x_{com} = \frac{1}{3} * 6 $$

$$ x_{com} = 2cm $$

Similarly:

$$ y_{com} = \frac{1}{M} * Sum m_{n}y_{n} $$

$$ y_{com} = \frac{1}{2 + 1} * (2)(2) + (1)(4) $$

$$ x_{com} = \frac{1}{3} * 8 $$

$$ x_{com} = 2.66cm $$

So, the required center of mass is given as follows:

$$ COM = \left(2, 2.66\right) $$

Which is our answer.

For the center of mass calculation in a three dimensional coordinate system, you can use a free online center of mass calculator 3D.

How Center Of Mass Calculator Works?

You can depict accurate results by fetching values to our free center of mass calculus calculator. What you need to do is described below.

Input:

• First of all, select the system that could be either 1D, 2D or 3D.

If you select 1D system:

• Select the number of masses which is upto 10.
• Write down the mass of each object.
• Also write its general position from the zero reference.
• Hit the calculate button.

If you select 2D system:

• Select the number of masses which is upto 10.
• Write down the mass of each object.
• Enter the value of x coordinates of both masses
• Also, enter the y coordinates of both the masses
• Click ‘calculate’

If you select 3D system:

• Select the number of masses which is upto 10.
• Write down the mass of each object.
• Enter x coordinates of each object.
• Similarly enter the y coordinates
• Enter the z coordinates in the same way
• Click ‘calculate’

Output:

The center of mass integral calculator finds:

• Center of mass for the objects given in various units of length.

FAQ’s:

Is the center of mass a reality?

No, the center of mass of any system is just a hypothetical point where the system becomes at rest.

What is the speed of center of mass?

all the individual masses have their own accelerations in a particular direction. But the center of mass has a fixed acceleration in the direction of the x coordinate which is about \(0.33 m/s^{2})\.

What do you mean by momentum of a body?

The product of mass and velocity of a body is called its momentum. It is a vector quantity having a particular direction and magnitude.

What are the dimensions of the center of mass?

As the SI unit of center of mass is meter(m), the dimensions of center of mass are in the direction of length as well which are [L].

Conclusion:

Center of mass has vast applications in the field of mechanics, aeronautics and aerospace where they are used to keep the aircrafts and spacecrafts in state of equilibrium. Professional scholars make vast use of a free online center of mass calculator to find the point of reference where the overall mass is pivoted.

References:

From the source of wikipedia: Barycentric coordinates, Center of gravity, Linear and angular momentum.

From the source of khan academy: Force vs. time graphs, conservation of momentum.

From the source of lumen learning: Internal and External Forces, Force and Momentum, Center of Mass and Conservation of Momentum, Center of Mass of Continuous Objects