Cubic Yard Calculator

The cubic yard calculator helps you find the volume of cement, mulch, concrete, or other landscape material in cubic yards. You can enter dimensions in multiple units available and the tool will function to calculate cubic yards for them.

With that, you can input values as whole numbers or decimals. The calculator will give you accurate results for your convenience.

How Much Is a Cubic Yard?

“A cubic yard is a cube with a length, width, and height of 1 yard”

1 Yard = 3 ft = 36 inches
1 Cubic Yards = 27 Cubic Feet (3 feet long, 3 feet wide, and 3 feet high)

Cubic Yard Measurements In Other Units:

1 cu yd =	1 yd x 1 yd x 1 yd
1 cu yd =	3 ft x 3 ft x 3 ft
1 cu yd =	36 in x 36 in x 36 in
1 cu yd =	0.9144 m x 0.9144 m x 0.9144 m
1 cu yd =	91.44 cm x 91.44 cm x 91.44 cm

Except for these standard measurements, you can get cubic yardage volume for any custom inputs with our cubic yard calculator.

How to Calculate Cubic Yards Using Feet and Inches?

First of all, measure the length, width, and depth of the area or container in feet
If you have measurements in feet and inches, divide inches by 12 to convert your readings to feet
Multiply all measured values in feet to get the cubic feet
At last, divide the result by 27 to calculate cubic yards

Mathematically:

Cu ft = [Length (ft) × Width (ft) × Height (ft)]/27

Cubic Yard Formulas For Different Shapes:

Rectangle The area of the rectangular area in (ft^2)= Length x Width The volume (ft^3)= Depth x Area The volume in cubic (yard^3)= (volume ft^3)/27
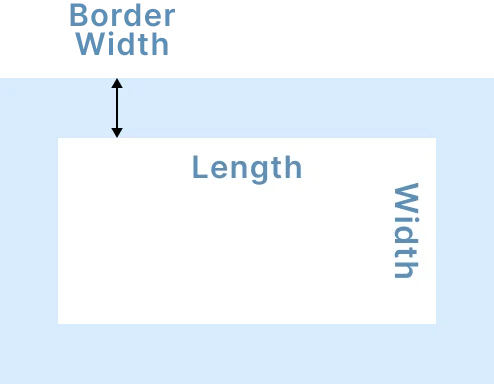Square The area of the square area in (ft^2)= 2 x Side length The volume (ft^3)= Depth x Area The volume in cubic (yard^3)= (volume ft^3)/27
Rectangular Border Area Inner Area (ft^2)= Length x Width Total area (ft^2) = Length+(2 x Border width)) x(Width +(2 x Border width)) Area (ft^2) = Total area- Inner area Volume (ft^3)= Depth x Area Volume in cubic (yard^3)= (volume ft^3)/27
Circle Area of the circle (ft^2)= Pi x radius^2 Where Pi=3.14 Volume (ft^3)= Depth x Area Volume in cubic (yard^3)= (volume ft^3)/27
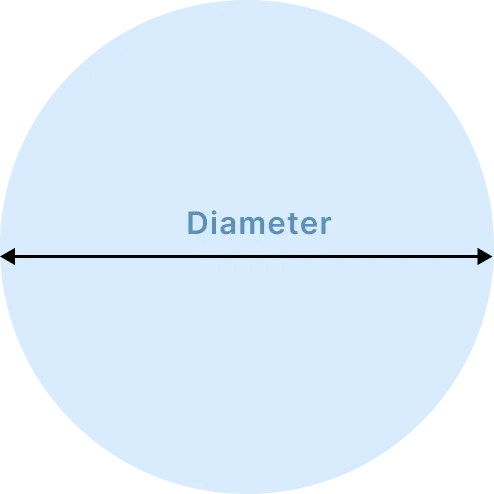Circular Border Area of the outer diameter(ft^2)= Inner diameter +(2x Border width) Outer area (ft^2)= Pi x outer radius^2 Inner (ft^2)= Pi x inner radius^2 Where Pi=3.14 Area (ft^2) = outer area- Inner area Volume (ft^3)= Depth x Area Volume in cubic (yard^3)= (volume ft^3)/27
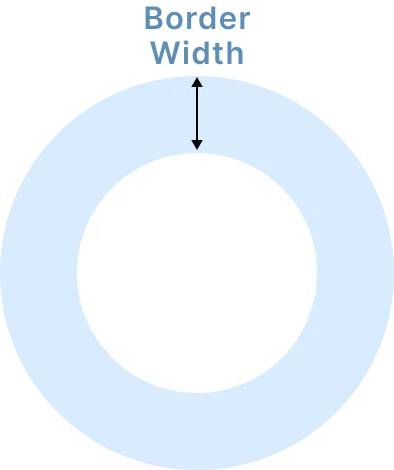Circular Annulus Area of the outer diameter(ft^2)= Inner diameter +(2x Border width) Outer area (ft^2)= Pi x outer radius^2 Inner (ft^2)= Pi x inner radius^2 Where Pi=3.14 Area (ft^2) = outer area- Inner area Volume (ft^3)= Depth x Area Volume in cubic (yard^3)= (volume ft^3)/27
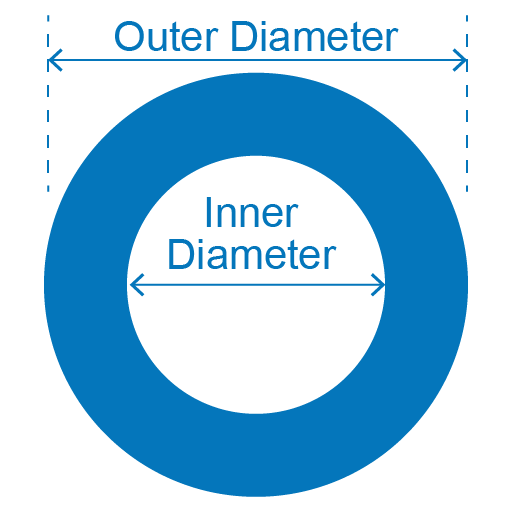Triangle Inner Area (ft^2)= (¼)x square root[ (a+b+c) x (b+c-a) x (c+a-b) x (a+b-c) ] Volume (ft^3)= Depth x Area Volume in cubic (yard^3)= (volume ft^3)/27
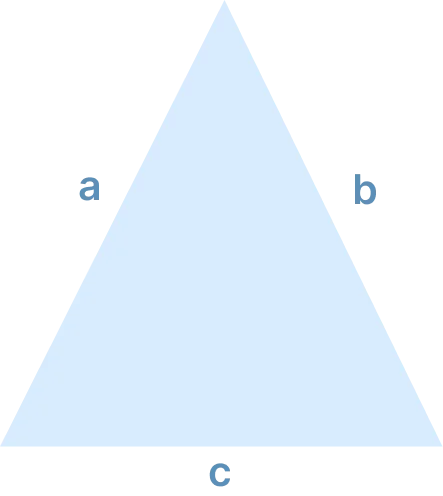Trapezoid Inner area (ft^2)= ((a + b) / 2 )h Volume (ft^3)= Depth x Area Volume in cubic (yard^3)= (volume ft^3)/27
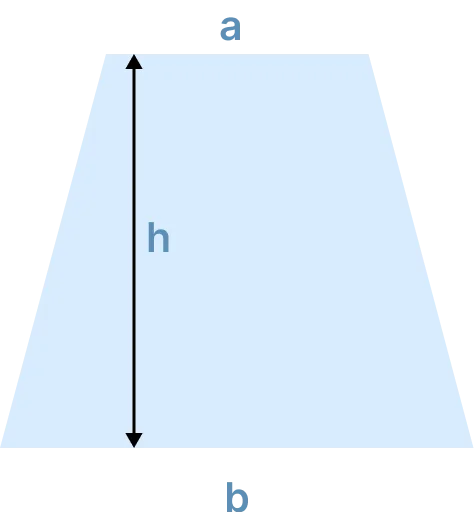Cube Volume (ft^3)=L^3 Volume in cubic (yard^3)= (volume ft^3)/27
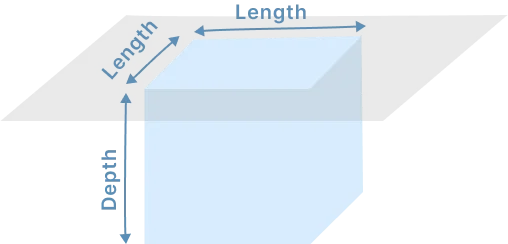Cylinder Circle area in (ft^2)= Pi x radius^2 x h Where Pi=3.14 Volume (ft^3)= Depth x Area Volume in cubic (yard^3)= (volume ft^3)/27
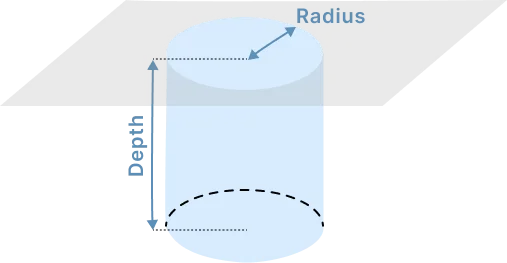Hollow Cylinder Area of the hollow cylinder in (ft^2)= π (R2 – r2) Where π =3.14 Volume (ft^3)= Depth x Area=π (R2 – r2) h Volume in cubic (yard^3)= (volume ft^3)/27
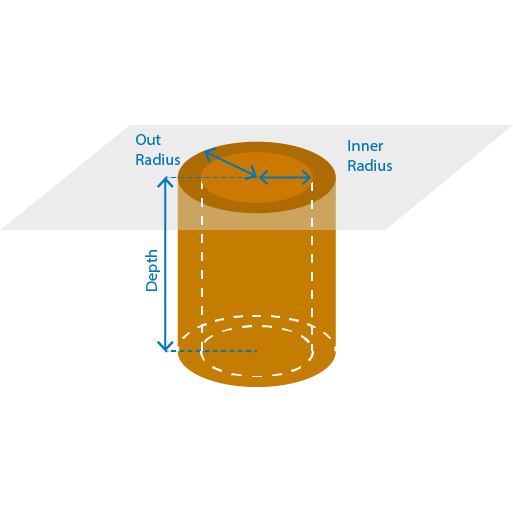Hemisphere Volume (ft^3)= V = (2/3)πr3 Volume in cubic (yard^3)= (volume ft^3)/27
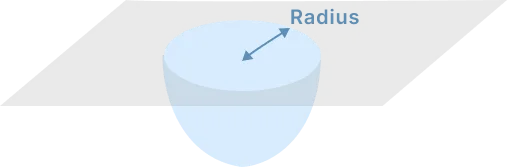Pyramid Volume (ft^3)= V = (1/3) (Base area x h) Volume in cubic (yard^3)= (volume ft^3)/27

Example:

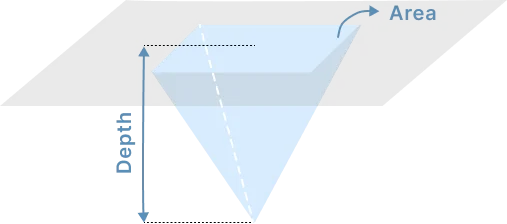How to find cubic yards for a land space with the following dimensions?

Length = 9 feet
Width = 17 feet
Depth = 4 inches

Solution:

Step # 01:

First of all, convert depth measurement to feet:

4 inches = 4/12 = 0.33 feet

Step # 02:

Calculating area in cubic feet:

Cubic Feet = Length (ft) × Width (ft) × Height (ft)

Cubic Feet = 9ft × 17ft × 0.33ft

Cubic Feet = 50.49 cu ft

Step # 03:

Calculating Cubic Yards:

Cubic Feet = [50.49 cu ft]/27

Cubic Yard= 1.87 cu yd

Is 1 Yard The Same As 1 Cubic Yard?

No! Where 1 yard is equal to 3 feet (36 inches), 1 Cubic yard is the volume of a cube with length, width, and height of 3 feet (36 inches) each.

How Many Yards of Concrete Do I Require For a 24×24 Slab?

You need around 7.11 yards.

Why Do We Need Cubic Yards?

Most of the materials used in the construction are measured in cubic yards. Among these include:

Concrete
Sand
Rock
Gravel
Fill dirt
Topsoil
Mulch
Compost

Cubic Feet To Cubic Yard Conversion:

Cubic Feet	Cubic Yards
1 ft³	0.037037 yd³
2 ft³	0.074074 yd³
3 ft³	0.111111 yd³
4 ft³	0.148148 yd³
5 ft³	0.185185 yd³
6 ft³	0.222222 yd³
7 ft³	0.259259 yd³
8 ft³	0.296296 yd³
9 ft³	0.333333 yd³
10 ft³	0.37037 yd³
11 ft³	0.407407 yd³
12 ft³	0.444444 yd³
13 ft³	0.481481 yd³
14 ft³	0.518519 yd³
15 ft³	0.555556 yd³
16 ft³	0.592593 yd³
17 ft³	0.62963 yd³
18 ft³	0.666667 yd³
19 ft³	0.703704 yd³
20 ft³	0.740741 yd³
21 ft³	0.777778 yd³
22 ft³	0.814815 yd³
23 ft³	0.851852 yd³
24 ft³	0.888889 yd³
25 ft³	0.925926 yd³
26 ft³	0.962963 yd³
27 ft³	1 yd³
28 ft³	1.037 yd³
29 ft³	1.0741 yd³
30 ft³	1.1111 yd³
31 ft³	1.1481 yd³
32 ft³	1.1852 yd³
33 ft³	1.2222 yd³
34 ft³	1.2593 yd³
35 ft³	1.2963 yd³
36 ft³	1.3333 yd³
37 ft³	1.3704 yd³
38 ft³	1.4074 yd³
39 ft³	1.4444 yd³
40 ft³	1.4815 yd³

1	What is priceeight Class?
2	priceeight Class Chart:
3	How to Calculate priceeight Density (Step by Step):
4	Factors that Determine priceeight Classification:
5	What is the purpose of priceeight Class?
6	Are mentioned priceeight Classes verified by the officials?
7	Are priceeight Classes of UPS and FedEx same?