Midpoint Calculator

The free midpoint calculator helps to find the distance and midpoint of a line segment and provides you with step-by-step calculations.

With the help of the midpoint coordinate calculator, you can find the missing midpoint coordinates between the given points along with the graphical representation. 

What Is The Midpoint of Line Segment?

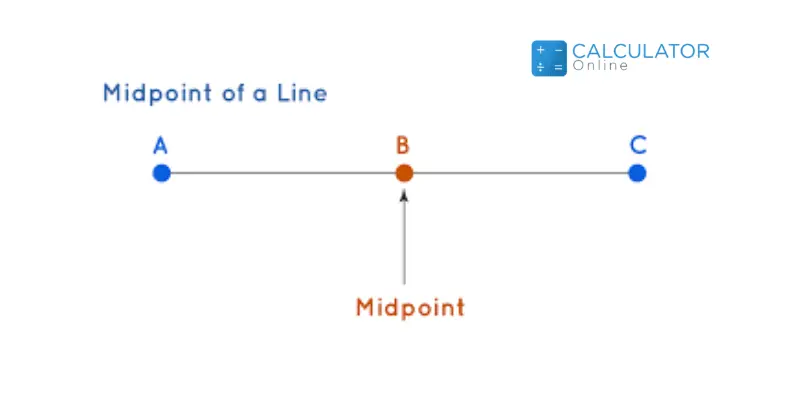
In geometry, the midpoint is referred to as a point that is halfway between two points of a line segment. More simply, it is said to be the middle point of the line segment.

The midpoint is one that divides the segment into two equal segments. If (x1, y1) and (x2, y2) are the two given endpoints of the line segment.

A midpoint exists with any two ordered pairs that lie exactly halfway between each ordered pair. Remember that this is accurate in two dimensions (x and y coordinates) and three dimensions (x, y, and z coordinates).

Regarding two dimensions, you only have two endpoints, midpoints and endpoints are correlated terms, so, try this missing endpoint calculator to find the endpoint of a line segment.

where;

• M indicates the midpoint
• \(\ x_{m}\ is\ the\ x-coordinate\ of \ midpoint\)
• \(\ y_{m}\ is\ the\ y-coordinate\ of \ midpoint\)

You can consider the distance calculator to find the distance among any two points, parallel or straight lines that have coordinates (x, y, z, k) in 1 to 4 dimensions.

How To Find The Midpoint?

Go through the below-mentioned steps to calculate the midpoint:

• First of all, name the coordinates of the two endpoints
• Sum the values of x and y separately
• Insert the resultant values in the midpoint equation as we have done in the following example 

Example:

Let’s suppose you have 2 endpoints having x-coordinates and y-coordinates as (2, 4) and (6, 8), find the midpoint.

Solution:

Given that:

Endpoint 1: (2, 4)

Endpoint 2: (6, 8)

By using the midpoint formula:

\( \ M =(\dfrac{x_{1} + x_{2}}{2},  \dfrac{y_{1} + y_{2}}{2})\)

\( \ M =(\dfrac{2 + 6}{2},  \dfrac{4 + 8}{2})\)

\( \ M =(\dfrac{8}{2},  \dfrac{12}{2})\)

Missing Midpoint = (4, 6)

How To Calculate The Distance Between Two Points?

If the endpoints of a line segment are known, then you can find the distance/length between them with the help of the following formula that is derived from the Pythagorean theorem. 

Example:

Suppose you have two points, A(2, 8) and B(8, 12), find the distance between 2 points.

Solution:

Given that:

\(\ x_{1} = 2, \  y_{1} = 8\ (Coordinates\ of\ Point \ A)\)

\(\ x_{2} = 8, \  y_{2} = 12 \ (Coordinates\ of\ Point\ B)\)

\(\ d = \sqrt {(x_{2} – x_{1})^2 + (y_{2} – y_{1})^2}\)

\(\ d = \sqrt {(8 – 2)^2 + (12 – 8)^2}\)

\(\ d = \sqrt {(6)^2 + (4)^2}\)

\(\ d = \sqrt {36 + 16}\)

\(\ d = \sqrt {52}\ or\ 7.21\)

FAQ’s :

What Is The Midpoint of 0 And 5?

Only 2.5! To find the midpoint between two numbers, you need to add the two numbers together and divide the answer by 2. In this case, \(\dfrac{0 + 5}{2}, \dfrac{5}{2} =\ 2.5\).

Do You Round Midpoints?

According to mathematical terms, the boundaries and midpoints should not be rounded off. Remember that these midpoint numbers work out to a value in the hundredths, and sometimes you need thousandths.