Arc Length Calculator

When any two following values are known, you can use the arc length calculator to calculate the length of an arc along with the other related measurements:

Central Angle and Radius
Radius and Segment Height
Radius and Sector Area
Radius and Chord Length
Central Angle and Diameter
Central Angle and Sector Area
Central Angle and Chord Length
Chord Length and Central Height

What Is Arc Length?

The length of an arc can be defined as the total distance between two points along a section of any curve. It depends on:

Sector Area
Chord
Radius of Circle

Arc Length Calculator

Calculation of the length of an irregular arc segment is known as rectification of a curve.

Arc Length Formula:

When the angle is equal to \( 360 \) degrees or \( 2π \), then the arc length will be equal to the circumference. It can be stated as:

\(L / θ = C / 2π\)
In the equation for the circumference \(C = 2πr\)
\(L / θ = 2πr / 2π\)
After division there will be only: \(L / θ = r\)
To calculate arc length, you have to multiply the radius by the central angle \(θ: L = r\times θ\)

How To Find The Arc Length?

There are 2 different ways to find a circle’s arc length which are:

In radians: To find arc length with radius the formula is as follows:

\(\ s = \theta\times\ r\)

In degrees: To find arch length degrees the formula will be:

\(\ s =\ 2 \pi\ r (\dfrac{\theta}{360°})\)

Also, you can use the arc length calculator for quick calculations.

Example:

If you have the following values, then find the sector area and length of arc?

\(\ Radius\ of\ circle \ (r) =\ 50\ cm\)

\(\ The\ Central\ Angle =\ \dfrac{\pi}{4}\)

Solution:

To find the arc length:

\(\ S = 50\times \dfrac{pi}{4} =\dfrac{25\pi}{2cm} =\ 39.32\ cm\)

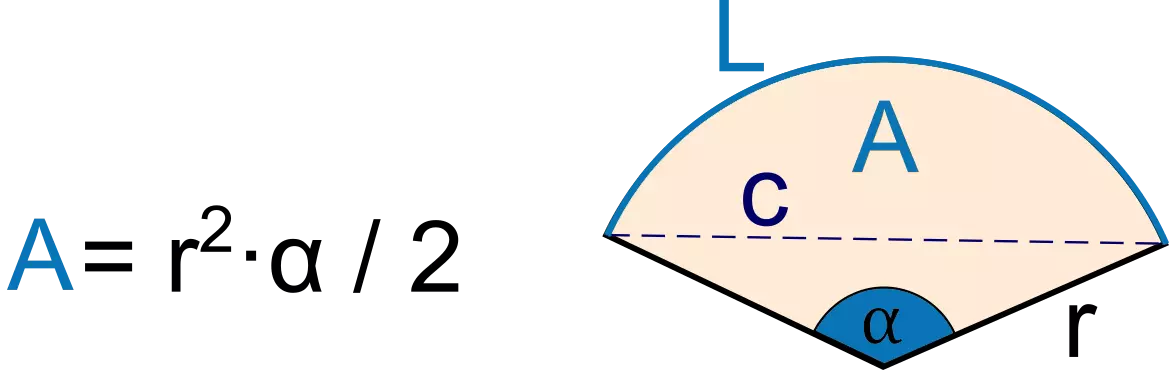
For Sector Area of the circle:

\(\ Area =\ A =\pi\ r^{2}=\ 3.1459\times \ 50^{2}= 7,864.75\ cm^{2}\)

How To Find Arc Length Using Sector Area And Central Angle?

If you have a sector area and the central angle, you can still calculate the arc of a circle. The formula is as follows:

\(\ L =\theta\times \sqrt(\dfrac{2A}{\theta})\)

Example:

Suppose the sector area is 300000 cm2 and the central angle is 60 degrees, Now how do you calculate an arc length without the radius of the circle? Let’s see how!

Solution:

\(\ 1\ centimeter^{2} =\dfrac{1}{10000}\ meter\ square\)

\(\ 300000\ cm^{2} =\dfrac{300000}{10000}\ meter\ square\)

\(\ 1\ degree =\dfrac{\pi}{180}\ radians\)

\(\ 60\ degrees =\ 60\times \dfrac{\pi}{180}\ radians =\ 1.0472\ rad\)

Now

\(\ Sector\ Area\ of\ Circle\ (A) =\ 30\ m^{2}\)

\(\ The\ Central\ Angle =\ 1.0472\ rad\)

\(\ L =\theta\times \sqrt(\dfrac{2A}{\theta})\)

\(\ L =\ 1.0472\times \sqrt(\dfrac{2(30)}{1.0472})\)

\(\ L =\ 1.0472\times \sqrt(\dfrac{60}{1.0472})\)

\(\ L =\ 1.0472\times \sqrt(57.295)\)

\(\ L =\ 1.0472\times \ 7.569\)

\(\ L =\ 7.926\ m\)

FAQ’s:

Is Arc Length The Same As The Angle?

No, the angle is the span between two radii of a circle, and on the other hand, the arc length is the distance between two radii along the curve.

What Is The Difference Between Chord Length And Arc Length?

The chord length is the straight line distance between two points, while an arc shows the total portion covered between two points(a segment of a circle).

References:

From the source of Wikipedia: Arc length, general approach.

1	What Is A Board Foot In Lumber (BF)?
2	Board Foot Formula:
3	Board Foot Units:
4	Important Thickness:
5	How To Calculate Board Feet?
6	What do you mean by the term “Surface Measure”?
7	What is meant by nominal measurement?
8	How do you define lineal measurement?