Nernst Equation Calculator

An online Nernst equation calculator can calculate the equilibrium potential for an ion based on its concentration and its charge. The standard cell potential for an electrochemical cell can be determined by finding the difference between the two half-cells reduction potentials. The cell potential should be positive for the whole reaction in order to be spontaneous. In this calculator, you will find rich information about the Nernst equation, reduction potential, and how to calculate equilibrium potential.

What is Nernst Equation?

The Nernst equation provides the relationship between the electrochemical cell potential, temperature, the standard cell potential, and the reaction quotient. The cell potentials can be determined by the Nernst equation even under non-standard conditions.
Usually, this equation is used to calculate the cell potential at any given pressure, reactant concentration, and temperature.

Nernst Equation for Electrode Potential:

$$ E_cell = E^0 – [RT / nf] ln Q $$

Where,

Q = Reaction Quotient

F = Faraday Constant

n = number of electrons in redox reaction

T = Temperature

R = Gas constant

\( E^0 \) = cell potential

\( E_cell \) = Cell Potential

We will use the Nernst equation calculator to find the electrode potential \( (E_red) \) from the standard electrode potential \( (E^0_{red}) \), for an ion is given by nernst equation.

For the reduction reaction, Nernst potential equation for electrode potential of the reduction reaction \( ne^– + M^{n+} → nM \) is;

$$ E_{red} = EM^{n+} / M = E^oM^{n+} / M – [2.303 RT / nF] log [1 / [Mn+]] $$

Where,
T = absolute temperature,
R = gas constant,
n = number of moles,
F = charged carried by one mole,
[Mn+] = active mass of the ions.

However, an online Ohm’s Law Calculator helps you to determine the relationship between current, resistance, and voltage across a given conductor.

Nernst Equilibrium Potential:

Here are some examples that tell how the Nernst equation calculator use equations to find the equilibrium potential for different ions:

The Nernst potential for Potassium \( K^+ (V_K) \) is:
$$ V_K = \frac {RT} {(+1) F} ln \frac { [K^+]_0 } {[K^+]_i} $$
The Nernst Equation for Chloride \( Cl^- (V_{Cl}) \) is:
$$ V_Cl = \frac {RT} {(+1) F} ln \frac { [Cl^+]_0 } {[Cl^+]_i} $$
The Netnst Equation Calcium \( Ca^{2+} (V_Ca) \) is:
$$ V_Ca = \frac {RT} {(+1) F} ln \frac { [Ca^+]_0 } {[Ca^+]_i} $$
And so on…

For a mammalian cell, its natural environment \( (37^o) \), the following potentials can be calculated. The Nernst calculator can be used to do all these calculations.

Nernst Equilibrium Potential Table:

How to Calculate Equilibrium Potential?

You can find the potential with an equilibrium potential calculator instantly, if you want to do all membrane potential calculations manually, then see an example below:

Example:

What will be the potential of 2M solution at the temperature of 300 Kelvin, when the zinc ions electrode potential is 0.76V.

Solution:

The Nernst equation for the given conditions is;

$$ EM^{n+} / M = E^o – log 1 / [Mn^+] x [(2.303RT) / nF] $$

Here,

\( E^° = 0.76V \)

\( [Mn^+]= 2 M \)

R =8.314 J/K mole

T =300 K

n = 2

F = 96500 C per mole

Now, you have to substitute all values in Nernst equation calculator that use all these values and display the potential values, you can also get the potential by substituting all the given values in the upper equation.

$$ EZn^{2+} / Zn = 0.76 – log 1/2 x [(2.303 × 300 x 8.314) / (96500 x 2)] = 0.76 – [(-0.301) x 0.0298] $$

$$ = 0.009 + 0.76 = 0.769V $$

Therefore, the potential of 2M solution at the temperature of 300 Kelvin is 0.769V.

Calculate Equilibrium Potential Constant:

When the products and reactants of the electrochemical cell reach equilibrium, the value of ΔG becomes 0. At this point, the equilibrium constant (Kc) and the reaction quotient are the same. Since ΔG = -nFE, the cell potential at this point is also zero.

By adding the values of E and Q into the Nernst equation, we get

$$ 0 = E^0_{cell} – (RT / nF) in K_c $$

The relationship between the equilibrium constant, Gibbs energy, and Nernst equation is illustrated below:

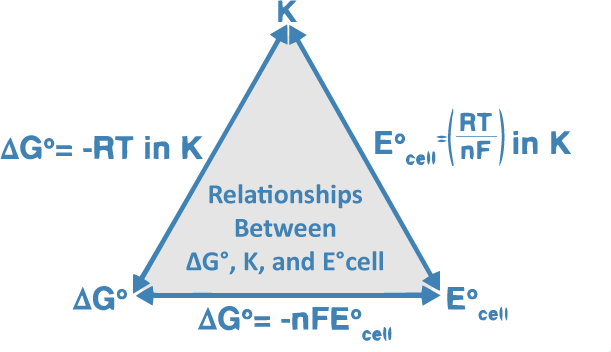
Converting the logarithm and substituting the standard temperature (T = 298K), the equation is transformed as:

$$ E^0_{cell} = (0.059 V / n) log K_c $$
$$ Log K_c = (nE^0_{cell}) / 0.059 V $$
Hence, the relationship between the equilibrium constant and standard cell potential is obtained. When calculating reversal potential the value of \( E^0_{cell} \) will hold the negative value, the K_c is less than 1 which suggests that the reaction is in the reverse direction will be favoured. Similarly, when do potential calculations with reversal potential calculator, the value of \( E^0_{cell} \) will be greater than zero and the \( K_c \) is greater than one, implying that the equilibrium favours the reaction in forwarding direction.

However, an online Photon Energy Calculator will help you to compute the energy of a photon from its frequency (f) and wavelength (ƛ).

Example:

How to calculate reversal potential and the concentration of silver ion, when copper concentration \( Cu^{2+} \) ion in a silver- copper electrochemical cell is 0.1M. If \(E^o(Cu^{2+}/Cu) = 0.34V, E^o(Ag^+ / Ag) = 0.8V \), and Cell potential is 0.422V.

Solution:

The standard potentials of the cell can be calculated by Nernst equation calculator by substituting the given electrode potentials or just add the values in equation, as shown below:

$$ E^o_{cell} = E^o_{cathode} – E^o_{anode} = 0.8V – 0.34V = 0.46V $$

Since the charge on the Ag ion is +1 and the charge on the Cu ion is +2, the balanced reaction of cell is:

$$ Cu + 2Ag^+ → Cu^{2+} + 2Ag $$

Since two electrons 2e are transferred in reaction, n = 2. Now, the equation for this cell can be written as:

$$ E_{cell} = E^0_{cell} – log(0.1 / [Ag^+]^2) x (0.059 / 2) $$
$$ 0.422V = 0.46 – (-1 – 2 log[Ag^+]) x 0.0296 $$

Hence, you can use the Log and Antilog Calculator for determine the logs and inverse log of any number base.

$$ -2log[Ag^+] = 1 + 1.283 = 2.283 $$
$$ log[Ag^+] = -1.141 $$
$$ [Ag^+] = antilog (-1.141) $$
$$ log[Ag^+] = 0.0722 M $$

Example:

Arrange all metals in order of their reducing power from the following potentials
$$ E^° = -0.76 V: Zn^{2+}_{(aq)} + 2e^– → Zn(s) $$
$$ E^° = -2.87 V: Ca^{2+}_{(aq)} + 2e^– → Ca(s) $$
$$ E^° = -0.25 V: Ni^{2+}_{(aq)} + 2e^– → Ni(s) $$
$$ E^° = -2.36 V: Mg^{2+}_{(aq)} + 2e^– → Mg(s) $$
$$ E^° = +0.25 V: Ni(s) → 2e^– + Ni^{2+}_{(aq)} $$

Arranging the potentials of reduction in increasing order provides the decreasing order of metals reducing power. Decreasing order of potentials is:

$$ Ca(-2.87) > Mg(-2.36V) > Zn (-0.76V) > Ni (-0.25V) $$

Nernst Equation Limitations:

In the dilute solution, the Nernst equation is represented in the form of concentrations since activity coefficients are close to the unity. But, at a higher concentration, the ion activities must be used. This complicates the Nernst equation since the estimation of non-ideal activities usually requires experimental measurements.

The Nernst equation only applies when there’s no net flow through an electrode. The ions activity changes when there is current flow, and there are additional resistive loss and overpotential terms that are contributing to the potential measurement.

At low concentrations of ions, the Nernst equation predicts the potential that approaches towards the ±∞. This is physically meaningless because exchange current density becomes low under certain conditions.

How does Nernst Equation Calculator Works?

An online equilibrium potential calculator computes the reduction potential of full-cell or half-cell reaction by following these steps:

Input:

• First, select any Nernst equation value that you want to calculate from the drop-down list.
• Now, substitute all given values in the related fields and select the Nernst equation units.
• Hit the “Calculate” button.

Output:

The Nernst potential calculator provides the calculations for:

• Cell potential of the cell (E_cell)
• Cell potential conditions (E^0)
• Universal Gas Constant (R)
• Temperature (T)
• Number of electrons transfer in redox reaction (n)
• Faraday Constant (F)
• Reaction Quotient (Q)

FAQs:

What are the applications of the Nernst Equation?

The equation of Nernst can be used to find:

• Oxidation potential at any condition
• EMF of an electrochemical cell
• Standard electrode potential
• Concentration of Unknown ionic

How does temperature affect the Nernst equation?

The potential of the cell is depending on the temperature, as the temperature of a Galvanic cell increases the cell potential decreases as other terms. An electron transformation and reaction quotient will remain the same for that particular cell. However, the temperature (T) does not have any effect on the Nernst equation but according to the equation, it is inversely proportional to the cell potential while other values and terms remain constant.

Define the Nernst equation at 25C.

The Nernst equation for 298 Kelvin can be represented as follows:
$$ E = E^0 – 0.0592/n log_10 Q $$
Hence, as per the Nernst equation, the potential of the electrochemical cell depends on the reaction quotient.

Conclusion:

Use this online Nernst equation calculator to determine the reduction potential in a cell with a basic electrochemistry equation. When designing electrochemical cells such as batteries, engineers and scientists should be able to compute electrical potentials with the Nernst equation to generate a powerful energy source.

Reference:

From the source of Wikipedia: Nernst equation, Nernst potential, Goldman equation, Using Boltzmann factor, Using thermodynamics (chemical potential).

From the source of Libre Text: Nernst Equation, Le Châtlier’s Principle, Reversible reaction, Redox reaction, Gibbs free energy.

From the source of University of Bristol: Conditions and Assumptions of Nernst, The effect of valency (the charge on the ion), Derivation of the Nernst Equation for Redox Reactions.